|
OpenFCST: The open-source Fuel Cell Simulation Toolbox
|
|
OpenFCST: The open-source Fuel Cell Simulation Toolbox
|
This class describes properties of gas mixtures. More...
#include <GasMixture.h>
Public Member Functions | |
Constructors, destructor, and initialization | |
| GasMixture () | |
| Constructor. More... | |
| GasMixture (const std::string &name) | |
| Constructor. More... | |
| virtual | ~GasMixture () |
| Destructor. More... | |
| virtual void | declare_parameters (ParameterHandler ¶m) const |
| Declare parameters. More... | |
| virtual void | initialize (ParameterHandler ¶m) |
| Initialize parameters. More... | |
| void | set_gases (const std::vector< PureGas * > &rgases) |
This function sets gases. More... | |
| void | set_total_pressure (const double &rtotal_pressure) |
This function takes a pressure (Pa) and if Isobaric fluid flow is set to true in the data file then the inputted pressure will be used else the DUMMY value is used. More... | |
| void | set_temperature (const double &rtemperature) |
This function takes a temperature (K) and if Isothermal fluid flow is set to true in the data file then the inputted temperature will be used else the DUMMY value is used. More... | |
Accessors and info | |
| unsigned int | n_gases () const |
| Function returning the number of gases in the mixture. More... | |
| PureGas * | get_gas (unsigned int &ind) const |
| Return gas stored in index ind. More... | |
| const std::vector< PureGas * > & | get_gases () const |
This function returns gases. More... | |
| const double & | get_total_pressure () const |
This function returns total_pressure. More... | |
| const double & | get_temperature () const |
This function returns temperature. More... | |
| virtual void | print_material_properties () const |
| This function prints out the material properties. More... | |
Service functions. Chapman Enskog isobaric diffusion coefficient. Binary gas mixture only. | |
| const double | get_ChapmanEnskog_isobaric_diffusion_coefficient () const |
This function returns Maxwell-Stefan isobaric diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant temperature. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant temperature. More... | |
| void | get_ChapmanEnskog_isobaric_diffusion_coefficient (std::vector< double > &diffusion_coefficient) const |
This function returns Maxwell-Stefan isobaric diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant temperature in the quadrature points of a mesh entity. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant temperature in the quadrature points of a mesh entity. More... | |
| const double | get_ChapmanEnskog_isobaric_diffusion_coefficient (const double &temperature) const |
This function returns Maxwell-Stefan isobaric diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable temperature. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable temperature. More... | |
| void | get_ChapmanEnskog_isobaric_diffusion_coefficient (const std::vector< double > &temperature, std::vector< double > &diffusion_coefficient) const |
This function returns Maxwell-Stefan isobaric diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable temperature in the quadrature points of a mesh entity. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable temperature in the quadrature points of a mesh entity. More... | |
Service functions. Derivatives of Chapman Enskog isobaric diffusion coefficient. Binary gas mixture only. | |
| const double | get_DChapmanEnskog_isobaric_diffusion_coefficient_Dtemperature (const double &temperature) const |
This function returns the first derivative 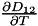 of the Maxwell-Stefan isobaric diffusion coefficient of gas of the Maxwell-Stefan isobaric diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable temperature. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable temperature. More... | |
| void | get_DChapmanEnskog_isobaric_diffusion_coefficient_Dtemperature (const std::vector< double > &temperature, std::vector< double > &dst) const |
This function returns the first derivative 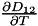 of the Maxwell-Stefan isobaric diffusion coefficient of gas of the Maxwell-Stefan isobaric diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable temperature in the quadrature points of a mesh entity. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable temperature in the quadrature points of a mesh entity. More... | |
Service functions. Chapman Enskog diffusion coefficient. Binary gas mixture only. | |
| const double | get_ChapmanEnskog_diffusion_coefficient () const |
This function returns Maxwell-Stefan diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and temperature. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and temperature. More... | |
| void | get_ChapmanEnskog_diffusion_coefficient (std::vector< double > &diffusion_coefficient) const |
This function returns Maxwell-Stefan diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and temperature in the quadrature points of a mesh entity. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and temperature in the quadrature points of a mesh entity. More... | |
| const double | get_ChapmanEnskog_diffusion_coefficient_at_constant_pressure (const double &temperature) const |
This function returns Maxwell-Stefan diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and variable temperature. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and variable temperature. More... | |
| void | get_ChapmanEnskog_diffusion_coefficient_at_constant_pressure (const std::vector< double > &temperature, std::vector< double > &diffusion_coefficient) const |
This function returns Maxwell-Stefan diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and variable temperature in the quadrature points of a mesh entity. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and variable temperature in the quadrature points of a mesh entity. More... | |
| const double | get_ChapmanEnskog_diffusion_coefficient_at_constant_temperature (const double &total_pressure) const |
This function returns Maxwell-Stefan diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and constant temperature. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and constant temperature. More... | |
| void | get_ChapmanEnskog_diffusion_coefficient_at_constant_temperature (const std::vector< double > &total_pressure, std::vector< double > &diffusion_coefficient) const |
This function returns Maxwell-Stefan diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and constant temperature in the quadrature points of a mesh entity. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and constant temperature in the quadrature points of a mesh entity. More... | |
| const double | get_ChapmanEnskog_diffusion_coefficient (const double &total_pressure, const double &temperature) const |
This function returns Maxwell-Stefan diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature. More... | |
| void | get_ChapmanEnskog_diffusion_coefficient (const std::vector< double > &total_pressure, const std::vector< double > &temperature, std::vector< double > &diffusion_coefficient) const |
This function returns Maxwell-Stefan diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature in the quadrature points of a mesh entity. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature in the quadrature points of a mesh entity. More... | |
Service functions. Derivatives of Chapman Enskog diffusion coefficient. Binary gas mixture only. | |
| const double | get_DChapmanEnskog_diffusion_coefficient_Dpressure (const double &total_pressure) const |
This function returns the first derivative 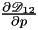 of the Maxwell-Stefan diffusion coefficient of gas of the Maxwell-Stefan diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and constant temperature. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and constant temperature. More... | |
| void | get_DChapmanEnskog_diffusion_coefficient_Dpressure (const std::vector< double > &total_pressure, std::vector< double > &dst) const |
This function returns the first derivative 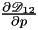 of the Maxwell-Stefan diffusion coefficient of gas of the Maxwell-Stefan diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and constant temperature in the quadrature points of a mesh entity. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and constant temperature in the quadrature points of a mesh entity. More... | |
| const double | get_DChapmanEnskog_diffusion_coefficient_Dpressure (const double &total_pressure, const double &temperature) const |
This function returns the first derivative 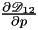 of the Maxwell-Stefan diffusion coefficient of gas of the Maxwell-Stefan diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature. More... | |
| void | get_DChapmanEnskog_diffusion_coefficient_Dpressure (const std::vector< double > &total_pressure, const std::vector< double > &temperature, std::vector< double > &dst) const |
This function returns the first derivative 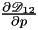 of the Maxwell-Stefan diffusion coefficient of gas of the Maxwell-Stefan diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature in the quadrature points of a mesh entity. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature in the quadrature points of a mesh entity. More... | |
| const double | get_DChapmanEnskog_diffusion_coefficient_Dtemperature (const double &temperature) const |
This function returns the first derivative 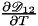 of the Maxwell-Stefan diffusion coefficient of gas of the Maxwell-Stefan diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and variable temperature. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and variable temperature. More... | |
| void | get_DChapmanEnskog_diffusion_coefficient_Dtemperature (const std::vector< double > &temperature, std::vector< double > &dst) const |
This function returns the first derivative 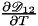 of the Maxwell-Stefan diffusion coefficient of gas of the Maxwell-Stefan diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and variable temperature in the quadrature points of a mesh entity. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and variable temperature in the quadrature points of a mesh entity. More... | |
| const double | get_DChapmanEnskog_diffusion_coefficient_Dtemperature (const double &total_pressure, const double &temperature) const |
This function returns the first derivative 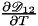 of the Maxwell-Stefan diffusion coefficient of gas of the Maxwell-Stefan diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature. More... | |
| void | get_DChapmanEnskog_diffusion_coefficient_Dtemperature (const std::vector< double > &total_pressure, const std::vector< double > &temperature, std::vector< double > &dst) const |
This function returns the first derivative 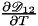 of the Maxwell-Stefan diffusion coefficient of gas of the Maxwell-Stefan diffusion coefficient of gas  in gas in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature in the quadrature points of a mesh entity. More... (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature in the quadrature points of a mesh entity. More... | |
Service functions. Chapman Enskog isobaric diffusion coefficients. Ternary and more complicated gas mixtures. | |
| const Table< 2, double > | get_ChapmanEnskog_isobaric_diffusion_coefficients () const |
This function returns Maxwell-Stefan isobaric diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant temperature. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant temperature. More... | |
| void | get_ChapmanEnskog_isobaric_diffusion_coefficients (std::vector< Table< 2, double > > &diffusion_coefficients) const |
This function returns Maxwell-Stefan isobaric diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant temperature in the quadrature points of a mesh entity. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant temperature in the quadrature points of a mesh entity. More... | |
| const Table< 2, double > | get_ChapmanEnskog_isobaric_diffusion_coefficients (const double &temperature) const |
This function returns Maxwell-Stefan isobaric diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable temperature. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable temperature. More... | |
| void | get_ChapmanEnskog_isobaric_diffusion_coefficients (const std::vector< double > &temperature, std::vector< Table< 2, double > > &diffusion_coefficients) const |
This function returns Maxwell-Stefan isobaric diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable temperature in the quadrature points of a mesh entity. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable temperature in the quadrature points of a mesh entity. More... | |
Service functions. Derivatives of Chapman Enskog isobaric diffusion coefficients. Ternary and more complicated gas mixtures. | |
| const Table< 2, double > | get_DChapmanEnskog_isobaric_diffusion_coefficients_Dtemperature (const double &temperature) const |
This function returns the first derivative 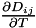 of the Maxwell-Stefan isobaric diffusion coefficients of gas of the Maxwell-Stefan isobaric diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable temperature. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable temperature. More... | |
| void | get_DChapmanEnskog_isobaric_diffusion_coefficients_Dtemperature (const std::vector< double > &temperature, std::vector< Table< 2, double > > &dst) const |
This function returns the first derivative 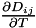 of the Maxwell-Stefan isobaric diffusion coefficients of gas of the Maxwell-Stefan isobaric diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable temperature in the quadrature points of a mesh entity. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable temperature in the quadrature points of a mesh entity. More... | |
Service functions. Chapman Enskog diffusion coefficients. Ternary and more complicated gas mixtures. | |
| const Table< 2, double > | get_ChapmanEnskog_diffusion_coefficients () const |
This function returns Maxwell-Stefan diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and temperature. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and temperature. More... | |
| void | get_ChapmanEnskog_diffusion_coefficients (std::vector< Table< 2, double > > &diffusion_coefficients) const |
This function returns Maxwell-Stefan diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and temperature in the quadrature points of a mesh entity. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and temperature in the quadrature points of a mesh entity. More... | |
| const Table< 2, double > | get_ChapmanEnskog_diffusion_coefficients_at_constant_pressure (const double &temperature) const |
This function returns Maxwell-Stefan diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and variable temperature. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and variable temperature. More... | |
| void | get_ChapmanEnskog_diffusion_coefficients_at_constant_pressure (const std::vector< double > &temperature, std::vector< Table< 2, double > > &diffusion_coefficients) const |
This function returns Maxwell-Stefan diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and variable temperature in the quadrature points of a mesh entity. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and variable temperature in the quadrature points of a mesh entity. More... | |
| const Table< 2, double > | get_ChapmanEnskog_diffusion_coefficients_at_constant_temperature (const double &total_pressure) const |
This function returns Maxwell-Stefan diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and constant temperature. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and constant temperature. More... | |
| void | get_ChapmanEnskog_diffusion_coefficients_at_constant_temperature (const std::vector< double > &total_pressure, std::vector< Table< 2, double > > &diffusion_coefficients) const |
This function returns Maxwell-Stefan diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and constant temperature in the quadrature points of a mesh entity. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and constant temperature in the quadrature points of a mesh entity. More... | |
| const Table< 2, double > | get_ChapmanEnskog_diffusion_coefficients (const double &total_pressure, const double &temperature) const |
This function returns Maxwell-Stefan diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature. More... | |
| void | get_ChapmanEnskog_diffusion_coefficients (const std::vector< double > &total_pressure, const std::vector< double > &temperature, std::vector< Table< 2, double > > &diffusion_coefficients) const |
This function returns Maxwell-Stefan diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature in the quadrature points of a mesh entity. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature in the quadrature points of a mesh entity. More... | |
Service functions. Derivatives of Chapman Enskog diffusion coefficients. Ternary and more complicated gas mixtures. | |
| const Table< 2, double > | get_DChapmanEnskog_diffusion_coefficients_Dpressure (const double &total_pressure) const |
This function returns the first derivative 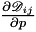 of the Maxwell-Stefan diffusion coefficients of gas of the Maxwell-Stefan diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and constant temperature. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and constant temperature. More... | |
| void | get_DChapmanEnskog_diffusion_coefficients_Dpressure (const std::vector< double > &total_pressure, std::vector< Table< 2, double > > &dst) const |
This function returns the first derivative 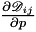 of the Maxwell-Stefan diffusion coefficients of gas of the Maxwell-Stefan diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and constant temperature in the quadrature points of a mesh entity. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and constant temperature in the quadrature points of a mesh entity. More... | |
| const Table< 2, double > | get_DChapmanEnskog_diffusion_coefficients_Dpressure (const double &total_pressure, const double &temperature) const |
This function returns the first derivative 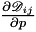 of the Maxwell-Stefan diffusion coefficients of gas of the Maxwell-Stefan diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature. More... | |
| void | get_DChapmanEnskog_diffusion_coefficients_Dpressure (const std::vector< double > &total_pressure, const std::vector< double > &temperature, std::vector< Table< 2, double > > &dst) const |
This function returns the first derivative 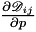 of the Maxwell-Stefan diffusion coefficients of gas of the Maxwell-Stefan diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature in the quadrature points of a mesh entity. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature in the quadrature points of a mesh entity. More... | |
| const Table< 2, double > | get_DChapmanEnskog_diffusion_coefficients_Dtemperature (const double &temperature) const |
This function returns the first derivative 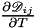 of the Maxwell-Stefan diffusion coefficients of gas of the Maxwell-Stefan diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and variable temperature. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and variable temperature. More... | |
| void | get_DChapmanEnskog_diffusion_coefficients_Dtemperature (const std::vector< double > &temperature, std::vector< Table< 2, double > > &dst) const |
This function returns the first derivative 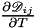 of the Maxwell-Stefan diffusion coefficients of gas of the Maxwell-Stefan diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and variable temperature in the quadrature points of a mesh entity. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and variable temperature in the quadrature points of a mesh entity. More... | |
| const Table< 2, double > | get_DChapmanEnskog_diffusion_coefficients_Dtemperature (const double &total_pressure, const double &temperature) const |
This function returns the first derivative 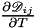 of the Maxwell-Stefan diffusion coefficients of gas of the Maxwell-Stefan diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature. More... | |
| void | get_DChapmanEnskog_diffusion_coefficients_Dtemperature (const std::vector< double > &total_pressure, const std::vector< double > &temperature, std::vector< Table< 2, double > > &dst) const |
This function returns the first derivative 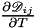 of the Maxwell-Stefan diffusion coefficients of gas of the Maxwell-Stefan diffusion coefficients of gas  in gas in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature in the quadrature points of a mesh entity. More... written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature in the quadrature points of a mesh entity. More... | |
Service functions. Calculate partial viscosity mixture | |
| const std::vector< std::vector < double > > | get_isothermal_nonisobaric_partial_viscosity (const double &tempOfMixture, const std::vector< std::vector< double > > &density, const std::vector< double > &molarMass, const std::vector< double > &dynamicViscosity, const std::vector< double > &collisionDiameter, const std::vector< double > &porosity, std::vector< std::vector< std::vector< double > > > ¶mMatrix, std::vector< FullMatrix< double > > &PInv) const |
| This function calculates the partial viscosity based on value stored in mixture_viscosity_mode and ASSUMES ISOTHERMAL and NONISOBARIC fluid flow. More... | |
| const std::vector< std::vector < double > > | get_nonisothermal_nonisobaric_partial_viscosity (const std::vector< double > &temperature, const std::vector< std::vector< double > > &density, const std::vector< double > &molarMass, const std::vector< std::vector< double > > &dynamicViscosity, const std::vector< double > &collisionDiameter, const std::vector< double > &porosity, std::vector< std::vector< std::vector< double > > > ¶mMatrix, std::vector< FullMatrix< double > > &PInv) const |
| This function calculates the partial viscosity based on value stored in mixture_viscosity_mode and ASSUMES NONISOTHERMAL and NONISOBARIC fluid flow. More... | |
| std::vector< double > | get_isothermal_nonisobaric_Wilke_partial_viscosity (const std::vector< double > &density, const std::vector< double > &dynamicViscosity, const std::vector< double > &molarMass, const double &porosity) const |
This is an overloaded function that calculates the Wilke partial viscosity model and ASSUMES ISOTHERMAL and NONISOBARIC fluid flow, but doesn't return the 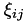 matrix. More... matrix. More... | |
| std::vector< double > | get_isothermal_nonisobaric_Wilke_partial_viscosity (const std::vector< double > &density, const std::vector< double > &dynamicViscosity, const std::vector< double > &molarMass, const double &porosity, std::vector< std::vector< double > > &xi) const |
| Same as another overloaded function (ASSUMES ISOTHERMAL and NONISOBARIC fluid flow). More... | |
| std::vector< double > | get_nonisothermal_nonisobaric_Wilke_partial_viscosity (const std::vector< double > &density, const std::vector< double > &dynamicViscosity, const std::vector< double > &molarMass, const double &porosity, std::vector< std::vector< double > > &xi) const |
| This function calculates the partial viscosity using the Wilke model based on value stored in mixture_viscosity_mode and ASSUMES NONISOTHERMAL and NONISOBARIC fluid flow. More... | |
| std::vector< double > | get_isothermal_nonisobaric_OmegaKG_partial_viscosity (const std::vector< double > &density, const std::vector< double > &collisionDiameter, const std::vector< double > &molarMass, const double &temperature, const double &porosity) const |
This is an overloaded function that calculates the Kerkhof and Geboers partial viscosity model based on the Omega integrals and ASSUMES ISOTHERMAL and NONISOBARIC fluid flow, but doesn't return the 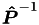 matrix or a table of the Omega integrals. More... matrix or a table of the Omega integrals. More... | |
| std::vector< double > | get_isothermal_nonisobaric_OmegaKG_partial_viscosity (const std::vector< double > &density, const std::vector< double > &collisionDiameter, const std::vector< double > &molarMass, const double &temperature, const double &porosity, std::vector< std::vector< double > > &omegaIntegralTable, FullMatrix< double > &PInv) const |
| Same as other overloaded function (ASSUMES ISOTHERMAL and NONISOBARIC fluid flow). More... | |
| std::vector< double > | get_nonisothermal_nonisobaric_OmegaKG_partial_viscosity (const std::vector< double > &density, const std::vector< double > &collisionDiameter, const std::vector< double > &molarMass, const double &temperature, const double &porosity, std::vector< std::vector< double > > &omegaIntegralTable, FullMatrix< double > &PInv) const |
| This function calculates the partial viscosity using the OmegaKG model based on value stored in mixture_viscosity_mode and ASSUMES NONISOTHERMAL and NONISOBARIC fluid flow. More... | |
| void | get_isothermal_nonisobaric_delta_partial_viscosity (const double &tempOfMixture, const std::vector< std::vector< std::vector< double > > > ¶mMatrix, const std::vector< FullMatrix< double > > &PInv, const std::vector< double > &porosity, const std::vector< double > &molarMass, const std::vector< double > &dynamicViscosity, const std::vector< double > &collisionDiameter, const std::vector< std::vector< std::vector< double > > > &deltaDensity, const std::vector< std::vector< double > > &density, std::vector< std::vector< std::vector< double > > > &deltaPartialViscosity) const |
| This function calculates the variation in partial viscosity based on value stored in mixture_viscosity_mode and ASSUMES ISOTHERMAL and NONISOBARIC fluid flow. More... | |
| void | get_nonisothermal_nonisobaric_delta_partial_viscosity (const std::vector< double > &temperature, const std::vector< std::vector< std::vector< double > > > ¶mMatrix, const std::vector< FullMatrix< double > > &PInv, const std::vector< double > &porosity, const std::vector< double > &molarMass, const std::vector< std::vector< double > > &dynamicViscosity, const std::vector< double > &collisionDiameter, const std::vector< std::vector< std::vector< double > > > &deltaDensity, const std::vector< std::vector< double > > &density, std::vector< std::vector< std::vector< double > > > &deltaPartialViscosity) const |
| This function calculates the variation in partial viscosity based on value stored in mixture_viscosity_mode and ASSUMES NONISOTHERMAL and NONISOBARIC fluid flow. More... | |
| void | get_Wilke_delta_partial_viscosity_wrt_density (const std::vector< std::vector< std::vector< double > > > &xi, const std::vector< double > &porosity, const std::vector< double > &molarMass, const std::vector< double > &dynamicViscosity, const std::vector< std::vector< std::vector< double > > > &deltaDensity, const std::vector< std::vector< double > > &density, std::vector< std::vector< std::vector< double > > > &deltaPartialViscosity) const |
| Calculates the variation in Wilke's partial viscosity model w.r.t. More... | |
| void | get_Wilke_delta_partial_viscosity_wrt_temperature (const std::vector< std::vector< std::vector< double > > > &xi, const std::vector< double > &porosity, const std::vector< double > &molarMass, const std::vector< double > &dynamicViscosity, const std::vector< std::vector< std::vector< double > > > &deltaTemperature, const std::vector< std::vector< double > > &density, std::vector< std::vector< std::vector< double > > > &deltaPartialViscosity) const |
| Calculates the variation in Wilke's partial viscosity model w.r.t. More... | |
| void | get_OmegaKG_delta_partial_viscosity_wrt_density (const double &tempOfMixture, const std::vector< std::vector< std::vector< double > > > &omegaIntegralTable, const std::vector< FullMatrix< double > > &PInv, const std::vector< double > &porosity, const std::vector< double > &molarMass, const std::vector< double > &collisionDiameter, const std::vector< std::vector< std::vector< double > > > &deltaDensity, const std::vector< std::vector< double > > &density, std::vector< std::vector< std::vector< double > > > &deltaPartialViscosity) const |
| Calculates the variation in Kerkhof and Geboers partial viscosity model using Omega integrals w.r.t. More... | |
| void | get_OmegaKG_delta_partial_viscosity_wrt_temperature (const std::vector< double > &temperature, const std::vector< std::vector< std::vector< double > > > &omegaIntegralTable, const std::vector< FullMatrix< double > > &PInv, const std::vector< double > &porosity, const std::vector< double > &molarMass, const std::vector< double > &collisionDiameter, const std::vector< std::vector< std::vector< double > > > &deltaDensity, const std::vector< std::vector< double > > &density, std::vector< std::vector< std::vector< double > > > &deltaPartialViscosity) const |
| Calculates the variation in Kerkhof and Geboers partial viscosity model using Omega integrals w.r.t. More... | |
| void | get_Null_delta_viscosity (std::vector< std::vector< std::vector< double > > > &deltaViscosity) const |
| Returns a std::vector< std::vector< std::vector<double> > > of 0s. More... | |
| void | get_delta_bulk_viscosity (const std::vector< PureGas * > &gases, const std::vector< std::vector< std::vector< double > > > &deltaPartialViscosity, std::vector< std::vector< std::vector< double > > > &deltaBulkViscosity) const |
| Loops through all variations of partial viscosity and calculates the varation in bulk viscosity according to bulk_viscosity_mode. More... | |
 Public Member Functions inherited from FuelCellShop::Material::BaseMaterial Public Member Functions inherited from FuelCellShop::Material::BaseMaterial | |
| void | set_derivative_flags (const std::vector< VariableNames > &flags) |
| Set the names of FCST solution variables with respect to which you would like to compute the derivatives of material properties. More... | |
| const std::string & | name_material () const |
| Return the name of the layer. More... | |
Protected Member Functions | |
Service functions. Binary collision integral. | |
| const double | get_binary_collision_integral (const unsigned int &N1=0, const unsigned int &N2=1) const |
| This function returns binary collision integral at a constant temperature. More... | |
| void | get_binary_collision_integral (std::vector< double > &binary_collision_integral, const unsigned int &N1=0, const unsigned int &N2=1) const |
| This function returns binary collision integral at a constant temperature in the quadrature points of a mesh entity. More... | |
| const double | get_binary_collision_integral (const double &temperature, const unsigned int &N1=0, const unsigned int &N2=1) const |
| This function returns binary collision integral at a variable temperature. More... | |
| void | get_binary_collision_integral (const std::vector< double > &temperature, std::vector< double > &binary_collision_integral, const unsigned int &N1=0, const unsigned int &N2=1) const |
| This function returns binary collision integral at a variable temperature in the quadrature points of a mesh entity. More... | |
| const double | get_Dbinary_collision_integral_Dtemperature (const double &temperature, const unsigned int &N1=0, const unsigned int &N2=1) const |
This function returns the first derivative 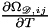 of the binary collision integral at a variable temperature. More... of the binary collision integral at a variable temperature. More... | |
| void | get_Dbinary_collision_integral_Dtemperature (const std::vector< double > &temperature, std::vector< double > &dst, const unsigned int &N1=0, const unsigned int &N2=1) const |
This function returns the first derivative 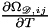 of the binary collision integral at a variable temperature in the quadrature points of a mesh entity. More... of the binary collision integral at a variable temperature in the quadrature points of a mesh entity. More... | |
Service functions. Omega* integrals. | |
| const double | get_omega_star_11_integral (const double &temperature, const unsigned int &N1=0, const unsigned int &N2=1) const |
This function returns 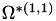 integral at a variable temperature. More... integral at a variable temperature. More... | |
| void | get_omega_star_11_integral (const double &temperature, std::vector< double > &omega_integral, const unsigned int &N1=0, const unsigned int &N2=1) const |
This function returns 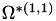 integral at a variable temperature in the quadrature points of a mesh entity. More... integral at a variable temperature in the quadrature points of a mesh entity. More... | |
| const double | get_omega_star_22_integral (const double &temperature, const unsigned int &N1=0, const unsigned int &N2=1) const |
This function returns 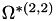 integral at a variable temperature. More... integral at a variable temperature. More... | |
| void | get_omega_star_22_integral (const double &temperature, std::vector< double > &omega_integral, const unsigned int &N1=0, const unsigned int &N2=1) const |
This function returns 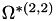 integral at a variable temperature in the quadrature points of a mesh entity. More... integral at a variable temperature in the quadrature points of a mesh entity. More... | |
 Protected Member Functions inherited from FuelCellShop::Material::BaseMaterial Protected Member Functions inherited from FuelCellShop::Material::BaseMaterial | |
| BaseMaterial () | |
| Constructor. More... | |
| BaseMaterial (const std::string &name) | |
| Constructor. More... | |
| virtual | ~BaseMaterial () |
| Destructor. More... | |
Protected Attributes | |
Fluid properties | |
| std::vector< PureGas * > | gases |
This std::vector contains all pure gases which form the whole gas mixture of a problem at hand. More... | |
| bool | tempIsoTherm = false |
This bool tells GasMisture if it should use isothermal assumption. More... | |
| bool | pressIsoBaric = false |
This bool tells GasMisture if it should use isobaric assumption. More... | |
| double | total_pressure = 1.0 |
Total pressure of the whole mixture, ![$ p_{\text{total}} \quad \left[ \text{Pa} \right] $](form_327.png) . More... . More... | |
| double | temperature = 1.0 |
Temperature of the whole gas mixture, ![$ T \quad \left[ \text{K} \right] $](form_328.png) . More... . More... | |
Names and modes | |
| std::string | mixture_viscosity_mode |
 Protected Attributes inherited from FuelCellShop::Material::BaseMaterial Protected Attributes inherited from FuelCellShop::Material::BaseMaterial | |
| const std::string | name |
| Name of the layer. More... | |
| std::vector< VariableNames > | derivative_flags |
| Flags for derivatives: These flags are used to request derivatives of material properties. More... | |
This class describes properties of gas mixtures.
This class contains the following data:
std::vector of pointers to the PureGas objects called gases,total_pressure,temperature.The whole gas mixture is supposed to be isobaric if some concrete value of total_pressure is assigned by either using the set_total_pressure() function or defining it in the parameters file.
If nothing happens, then the value of total_pressure gets the DUMMY number equal 1.e300 and the whole gas mixture is treated as non-isobaric. In this case, the total pressure of the whole gas mixture is one of the solution variables.
The whole gas mixture is supposed to be isothermal if some concrete value of temperature is assigned by either using the set_temperature() function or defining it in the parameters file.
If nothing happens, then the value of temperature gets the DUMMY number equal 1.e300 and the whole gas mixture is treated as non-isothermal. In this case, the temperature of the whole gas mixture is one of the solution variables.
NOTE: after calling initialize() please call set_total_pressure() and set_temperature() to insert the pressure and temperature from the Operating Conditions class if fluid flow is NOT isobaric or isothermal respectively. See these function calls below for more detail.
The following methods are used to compute the gas mixture properties:
 in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only),
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only), ![$ \quad \left[ \frac{\text{Pa } \text{m}^2}{\text{sec}} \right] \quad $](form_302.png)
 and partial derivative
and partial derivative 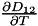 where the binary collision integral
where the binary collision integral 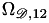 is given by
is given by 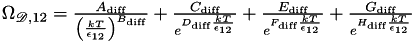
 in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only),
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only), ![$ \quad \left[ \frac{\text{m}^2}{\text{sec}} \right] \quad $](form_307.png)
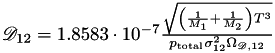 and partial derivatives
and partial derivatives 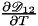 and
and 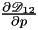 where the binary collision integral
where the binary collision integral 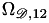 is given above
is given above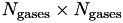 containing Maxwell-Stefan isobaric diffusion coefficients of gas
containing Maxwell-Stefan isobaric diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures),
written in the Chapman Enskog form (ternary and more complicated gas mixtures), ![$ \quad \left[ \frac{\text{Pa } \text{m}^2}{\text{sec}} \right] \quad $](form_302.png)
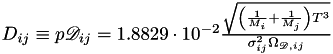 and partial derivatives
and partial derivatives 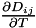 where the binary collision integral
where the binary collision integral 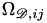 is given by
is given by 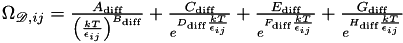
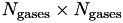 containing Maxwell-Stefan diffusion coefficients of gas
containing Maxwell-Stefan diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures),
written in the Chapman Enskog form (ternary and more complicated gas mixtures), ![$ \quad \left[ \frac{\text{m}^2}{\text{sec}} \right] \quad $](form_307.png)
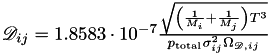 and partial derivatives
and partial derivatives 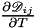 and
and 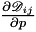 where the binary collision integral
where the binary collision integral 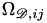 is given above
is given aboveFor developers: please update this info appropriately if you add a new method.
| FuelCellShop::Material::GasMixture::GasMixture | ( | ) |
Constructor.
| FuelCellShop::Material::GasMixture::GasMixture | ( | const std::string & | name | ) |
Constructor.
|
virtual |
Destructor.
|
virtual |
Declare parameters.
Reimplemented from FuelCellShop::Material::BaseMaterial.
|
protected |
This function returns binary collision integral at a constant temperature.
| N1 | - number of the first gas from gases, |
| N2 | - number of the second gas from gases. |
|
protected |
This function returns binary collision integral at a constant temperature in the quadrature points of a mesh entity.
| binary_collision_integral | - binary collision integral at a constant temperature in the quadrature points of a mesh entity, |
| N1 | - number of the first gas from gases, |
| N2 | - number of the second gas from gases. |
|
protected |
This function returns binary collision integral at a variable temperature.
| temperature | - temperature, |
| N1 | - number of the first gas from gases, |
| N2 | - number of the second gas from gases. |
|
protected |
This function returns binary collision integral at a variable temperature in the quadrature points of a mesh entity.
| temperature | - temperature in the quadrature points of a mesh entity, |
| binary_collision_integral | - binary collision integral at a variable temperature in the quadrature points of a mesh entity, |
| N1 | - number of the first gas from gases, |
| N2 | - number of the second gas from gases. |
| const double FuelCellShop::Material::GasMixture::get_ChapmanEnskog_diffusion_coefficient | ( | ) | const |
This function returns Maxwell-Stefan diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and temperature.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and temperature.
| void FuelCellShop::Material::GasMixture::get_ChapmanEnskog_diffusion_coefficient | ( | std::vector< double > & | diffusion_coefficient | ) | const |
This function returns Maxwell-Stefan diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and temperature in the quadrature points of a mesh entity.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and temperature in the quadrature points of a mesh entity.
| diffusion_coefficient | - Chapman Enskog diffusion coefficient at a constant total pressure and temperature in the quadrature points of a mesh entity. |
| const double FuelCellShop::Material::GasMixture::get_ChapmanEnskog_diffusion_coefficient | ( | const double & | total_pressure, |
| const double & | temperature | ||
| ) | const |
This function returns Maxwell-Stefan diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature.
| total_pressure | - total pressure, |
| temperature | - temperature. |
| void FuelCellShop::Material::GasMixture::get_ChapmanEnskog_diffusion_coefficient | ( | const std::vector< double > & | total_pressure, |
| const std::vector< double > & | temperature, | ||
| std::vector< double > & | diffusion_coefficient | ||
| ) | const |
This function returns Maxwell-Stefan diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature in the quadrature points of a mesh entity.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature in the quadrature points of a mesh entity.
| total_pressure | - total pressure in the quadrature points of a mesh entity, |
| temperature | - temperature in the quadrature points of a mesh entity, |
| diffusion_coefficient | - Chapman Enskog diffusion coefficient at a variable total pressure and temperature in the quadrature points of a mesh entity. |
| const double FuelCellShop::Material::GasMixture::get_ChapmanEnskog_diffusion_coefficient_at_constant_pressure | ( | const double & | temperature | ) | const |
This function returns Maxwell-Stefan diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and variable temperature.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and variable temperature.
| temperature | - temperature. |
| void FuelCellShop::Material::GasMixture::get_ChapmanEnskog_diffusion_coefficient_at_constant_pressure | ( | const std::vector< double > & | temperature, |
| std::vector< double > & | diffusion_coefficient | ||
| ) | const |
This function returns Maxwell-Stefan diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and variable temperature in the quadrature points of a mesh entity.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and variable temperature in the quadrature points of a mesh entity.
| temperature | - temperature in the quadrature points of a mesh entity, |
| diffusion_coefficient | - Chapman Enskog diffusion coefficient at a constant total pressure and variable temperature in the quadrature points of a mesh entity. |
| const double FuelCellShop::Material::GasMixture::get_ChapmanEnskog_diffusion_coefficient_at_constant_temperature | ( | const double & | total_pressure | ) | const |
This function returns Maxwell-Stefan diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and constant temperature.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and constant temperature.
| total_pressure | - total pressure. |
| void FuelCellShop::Material::GasMixture::get_ChapmanEnskog_diffusion_coefficient_at_constant_temperature | ( | const std::vector< double > & | total_pressure, |
| std::vector< double > & | diffusion_coefficient | ||
| ) | const |
This function returns Maxwell-Stefan diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and constant temperature in the quadrature points of a mesh entity.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and constant temperature in the quadrature points of a mesh entity.
| total_pressure | - total pressure in the quadrature points of a mesh entity, |
| diffusion_coefficient | - Chapman Enskog diffusion coefficient at a variable total pressure and constant temperature in the quadrature points of a mesh entity. |
| const Table< 2, double > FuelCellShop::Material::GasMixture::get_ChapmanEnskog_diffusion_coefficients | ( | ) | const |
This function returns Maxwell-Stefan diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and temperature.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and temperature.
| void FuelCellShop::Material::GasMixture::get_ChapmanEnskog_diffusion_coefficients | ( | std::vector< Table< 2, double > > & | diffusion_coefficients | ) | const |
This function returns Maxwell-Stefan diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and temperature in the quadrature points of a mesh entity.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and temperature in the quadrature points of a mesh entity.
| diffusion_coefficients | - Chapman Enskog diffusion coefficients at a constant total pressure and temperature in the quadrature points of a mesh entity. |
| const Table< 2, double > FuelCellShop::Material::GasMixture::get_ChapmanEnskog_diffusion_coefficients | ( | const double & | total_pressure, |
| const double & | temperature | ||
| ) | const |
This function returns Maxwell-Stefan diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature.
| total_pressure | - total pressure, |
| temperature | - temperature. |
| void FuelCellShop::Material::GasMixture::get_ChapmanEnskog_diffusion_coefficients | ( | const std::vector< double > & | total_pressure, |
| const std::vector< double > & | temperature, | ||
| std::vector< Table< 2, double > > & | diffusion_coefficients | ||
| ) | const |
This function returns Maxwell-Stefan diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature in the quadrature points of a mesh entity.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature in the quadrature points of a mesh entity.
| total_pressure | - total pressure in the quadrature points of a mesh entity, |
| temperature | - temperature in the quadrature points of a mesh entity, |
| diffusion_coefficients | - Chapman Enskog diffusion coefficients at a variable total pressure and temperature in the quadrature points of a mesh entity. |
| const Table< 2, double > FuelCellShop::Material::GasMixture::get_ChapmanEnskog_diffusion_coefficients_at_constant_pressure | ( | const double & | temperature | ) | const |
This function returns Maxwell-Stefan diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and variable temperature.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and variable temperature.
| temperature | - temperature. |
| void FuelCellShop::Material::GasMixture::get_ChapmanEnskog_diffusion_coefficients_at_constant_pressure | ( | const std::vector< double > & | temperature, |
| std::vector< Table< 2, double > > & | diffusion_coefficients | ||
| ) | const |
This function returns Maxwell-Stefan diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and variable temperature in the quadrature points of a mesh entity.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and variable temperature in the quadrature points of a mesh entity.
| temperature | - temperature in the quadrature points of a mesh entity, |
| diffusion_coefficients | - Chapman Enskog diffusion coefficients at a constant total pressure and variable temperature in the quadrature points of a mesh entity. |
| const Table< 2, double > FuelCellShop::Material::GasMixture::get_ChapmanEnskog_diffusion_coefficients_at_constant_temperature | ( | const double & | total_pressure | ) | const |
This function returns Maxwell-Stefan diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and constant temperature.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and constant temperature.
| total_pressure | - total pressure. |
| void FuelCellShop::Material::GasMixture::get_ChapmanEnskog_diffusion_coefficients_at_constant_temperature | ( | const std::vector< double > & | total_pressure, |
| std::vector< Table< 2, double > > & | diffusion_coefficients | ||
| ) | const |
This function returns Maxwell-Stefan diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and constant temperature in the quadrature points of a mesh entity.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and constant temperature in the quadrature points of a mesh entity.
| total_pressure | - total pressure in the quadrature points of a mesh entity, |
| diffusion_coefficients | - Chapman Enskog diffusion coefficients at a variable total pressure and constant temperature in the quadrature points of a mesh entity. |
| const double FuelCellShop::Material::GasMixture::get_ChapmanEnskog_isobaric_diffusion_coefficient | ( | ) | const |
This function returns Maxwell-Stefan isobaric diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant temperature.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant temperature.
| void FuelCellShop::Material::GasMixture::get_ChapmanEnskog_isobaric_diffusion_coefficient | ( | std::vector< double > & | diffusion_coefficient | ) | const |
This function returns Maxwell-Stefan isobaric diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant temperature in the quadrature points of a mesh entity.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant temperature in the quadrature points of a mesh entity.
| diffusion_coefficient | - Chapman Enskog isobaric diffusion coefficient at a constant temperature in the quadrature points of a mesh entity. |
| const double FuelCellShop::Material::GasMixture::get_ChapmanEnskog_isobaric_diffusion_coefficient | ( | const double & | temperature | ) | const |
This function returns Maxwell-Stefan isobaric diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable temperature.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable temperature.
| temperature | - temperature. |
| void FuelCellShop::Material::GasMixture::get_ChapmanEnskog_isobaric_diffusion_coefficient | ( | const std::vector< double > & | temperature, |
| std::vector< double > & | diffusion_coefficient | ||
| ) | const |
This function returns Maxwell-Stefan isobaric diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable temperature in the quadrature points of a mesh entity.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable temperature in the quadrature points of a mesh entity.
| temperature | - temperature in the quadrature points of a mesh entity, |
| diffusion_coefficient | - Chapman Enskog isobaric diffusion coefficient at a variable temperature in the quadrature points of a mesh entity. |
| const Table< 2, double > FuelCellShop::Material::GasMixture::get_ChapmanEnskog_isobaric_diffusion_coefficients | ( | ) | const |
This function returns Maxwell-Stefan isobaric diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant temperature.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant temperature.
| void FuelCellShop::Material::GasMixture::get_ChapmanEnskog_isobaric_diffusion_coefficients | ( | std::vector< Table< 2, double > > & | diffusion_coefficients | ) | const |
This function returns Maxwell-Stefan isobaric diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant temperature in the quadrature points of a mesh entity.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant temperature in the quadrature points of a mesh entity.
| diffusion_coefficients | - Chapman Enskog isobaric diffusion coefficients at a constant temperature in the quadrature points of a mesh entity. |
| const Table< 2, double > FuelCellShop::Material::GasMixture::get_ChapmanEnskog_isobaric_diffusion_coefficients | ( | const double & | temperature | ) | const |
This function returns Maxwell-Stefan isobaric diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable temperature.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable temperature.
| temperature | - temperature. |
| void FuelCellShop::Material::GasMixture::get_ChapmanEnskog_isobaric_diffusion_coefficients | ( | const std::vector< double > & | temperature, |
| std::vector< Table< 2, double > > & | diffusion_coefficients | ||
| ) | const |
This function returns Maxwell-Stefan isobaric diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable temperature in the quadrature points of a mesh entity.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable temperature in the quadrature points of a mesh entity.
| temperature | - temperature in the quadrature points of a mesh entity, |
| diffusion_coefficients | - Chapman Enskog isobaric diffusion coefficients at a variable temperature in the quadrature points of a mesh entity. |
|
protected |
This function returns the first derivative 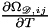 of the binary collision integral at a variable temperature.
of the binary collision integral at a variable temperature.
| temperature | - temperature, |
| N1 | - number of the first gas from gases, |
| N2 | - number of the second gas from gases. |
|
protected |
This function returns the first derivative 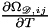 of the binary collision integral at a variable temperature in the quadrature points of a mesh entity.
of the binary collision integral at a variable temperature in the quadrature points of a mesh entity.
| temperature | - temperature in the quadrature points of a mesh entity, |
| dst | - 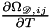 at a variable temperature in the quadrature points of a mesh entity, at a variable temperature in the quadrature points of a mesh entity, |
| N1 | - number of the first gas from gases, |
| N2 | - number of the second gas from gases. |
| const double FuelCellShop::Material::GasMixture::get_DChapmanEnskog_diffusion_coefficient_Dpressure | ( | const double & | total_pressure | ) | const |
This function returns the first derivative 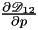 of the Maxwell-Stefan diffusion coefficient of gas
of the Maxwell-Stefan diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and constant temperature.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and constant temperature.
| total_pressure | - total pressure. |
| void FuelCellShop::Material::GasMixture::get_DChapmanEnskog_diffusion_coefficient_Dpressure | ( | const std::vector< double > & | total_pressure, |
| std::vector< double > & | dst | ||
| ) | const |
This function returns the first derivative 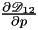 of the Maxwell-Stefan diffusion coefficient of gas
of the Maxwell-Stefan diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and constant temperature in the quadrature points of a mesh entity.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and constant temperature in the quadrature points of a mesh entity.
| total_pressure | - total pressure in the quadrature points of a mesh entity, |
| dst | - 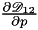 at a variable total pressure and constant temperature in the quadrature points of a mesh entity. at a variable total pressure and constant temperature in the quadrature points of a mesh entity. |
| const double FuelCellShop::Material::GasMixture::get_DChapmanEnskog_diffusion_coefficient_Dpressure | ( | const double & | total_pressure, |
| const double & | temperature | ||
| ) | const |
This function returns the first derivative 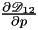 of the Maxwell-Stefan diffusion coefficient of gas
of the Maxwell-Stefan diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature.
| total_pressure | - total pressure, |
| temperature | - temperature. |
| void FuelCellShop::Material::GasMixture::get_DChapmanEnskog_diffusion_coefficient_Dpressure | ( | const std::vector< double > & | total_pressure, |
| const std::vector< double > & | temperature, | ||
| std::vector< double > & | dst | ||
| ) | const |
This function returns the first derivative 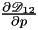 of the Maxwell-Stefan diffusion coefficient of gas
of the Maxwell-Stefan diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature in the quadrature points of a mesh entity.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature in the quadrature points of a mesh entity.
| total_pressure | - total pressure in the quadrature points of a mesh entity, |
| temperature | - temperature in the quadrature points of a mesh entity, |
| dst | - 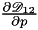 at a variable total pressure and temperature in the quadrature points of a mesh entity. at a variable total pressure and temperature in the quadrature points of a mesh entity. |
| const double FuelCellShop::Material::GasMixture::get_DChapmanEnskog_diffusion_coefficient_Dtemperature | ( | const double & | temperature | ) | const |
This function returns the first derivative 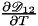 of the Maxwell-Stefan diffusion coefficient of gas
of the Maxwell-Stefan diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and variable temperature.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and variable temperature.
| temperature | - temperature. |
| void FuelCellShop::Material::GasMixture::get_DChapmanEnskog_diffusion_coefficient_Dtemperature | ( | const std::vector< double > & | temperature, |
| std::vector< double > & | dst | ||
| ) | const |
This function returns the first derivative 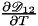 of the Maxwell-Stefan diffusion coefficient of gas
of the Maxwell-Stefan diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and variable temperature in the quadrature points of a mesh entity.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a constant total pressure and variable temperature in the quadrature points of a mesh entity.
| temperature | - temperature in the quadrature points of a mesh entity, |
| dst | - 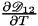 at a constant total pressure and variable temperature in the quadrature points of a mesh entity. at a constant total pressure and variable temperature in the quadrature points of a mesh entity. |
| const double FuelCellShop::Material::GasMixture::get_DChapmanEnskog_diffusion_coefficient_Dtemperature | ( | const double & | total_pressure, |
| const double & | temperature | ||
| ) | const |
This function returns the first derivative 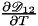 of the Maxwell-Stefan diffusion coefficient of gas
of the Maxwell-Stefan diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature.
| total_pressure | - total pressure, |
| temperature | - temperature. |
| void FuelCellShop::Material::GasMixture::get_DChapmanEnskog_diffusion_coefficient_Dtemperature | ( | const std::vector< double > & | total_pressure, |
| const std::vector< double > & | temperature, | ||
| std::vector< double > & | dst | ||
| ) | const |
This function returns the first derivative 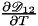 of the Maxwell-Stefan diffusion coefficient of gas
of the Maxwell-Stefan diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature in the quadrature points of a mesh entity.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable total pressure and temperature in the quadrature points of a mesh entity.
| total_pressure | - total pressure in the quadrature points of a mesh entity, |
| temperature | - temperature in the quadrature points of a mesh entity, |
| dst | - 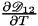 at a variable total pressure and temperature in the quadrature points of a mesh entity. at a variable total pressure and temperature in the quadrature points of a mesh entity. |
| const Table< 2, double > FuelCellShop::Material::GasMixture::get_DChapmanEnskog_diffusion_coefficients_Dpressure | ( | const double & | total_pressure | ) | const |
This function returns the first derivative 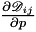 of the Maxwell-Stefan diffusion coefficients of gas
of the Maxwell-Stefan diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and constant temperature.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and constant temperature.
| total_pressure | - total pressure. |
| void FuelCellShop::Material::GasMixture::get_DChapmanEnskog_diffusion_coefficients_Dpressure | ( | const std::vector< double > & | total_pressure, |
| std::vector< Table< 2, double > > & | dst | ||
| ) | const |
This function returns the first derivative 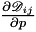 of the Maxwell-Stefan diffusion coefficients of gas
of the Maxwell-Stefan diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and constant temperature in the quadrature points of a mesh entity.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and constant temperature in the quadrature points of a mesh entity.
| total_pressure | - total pressure in the quadrature points of a mesh entity, |
| dst | - 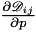 at a variable total pressure and constant temperature in the quadrature points of a mesh entity. at a variable total pressure and constant temperature in the quadrature points of a mesh entity. |
| const Table< 2, double > FuelCellShop::Material::GasMixture::get_DChapmanEnskog_diffusion_coefficients_Dpressure | ( | const double & | total_pressure, |
| const double & | temperature | ||
| ) | const |
This function returns the first derivative 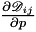 of the Maxwell-Stefan diffusion coefficients of gas
of the Maxwell-Stefan diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature.
| total_pressure | - total pressure, |
| temperature | - temperature. |
| void FuelCellShop::Material::GasMixture::get_DChapmanEnskog_diffusion_coefficients_Dpressure | ( | const std::vector< double > & | total_pressure, |
| const std::vector< double > & | temperature, | ||
| std::vector< Table< 2, double > > & | dst | ||
| ) | const |
This function returns the first derivative 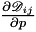 of the Maxwell-Stefan diffusion coefficients of gas
of the Maxwell-Stefan diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature in the quadrature points of a mesh entity.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature in the quadrature points of a mesh entity.
| total_pressure | - total pressure in the quadrature points of a mesh entity, |
| temperature | - temperature in the quadrature points of a mesh entity, |
| dst | - 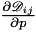 at a variable total pressure and temperature in the quadrature points of a mesh entity. at a variable total pressure and temperature in the quadrature points of a mesh entity. |
| const Table< 2, double > FuelCellShop::Material::GasMixture::get_DChapmanEnskog_diffusion_coefficients_Dtemperature | ( | const double & | temperature | ) | const |
This function returns the first derivative 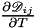 of the Maxwell-Stefan diffusion coefficients of gas
of the Maxwell-Stefan diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and variable temperature.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and variable temperature.
| temperature | - temperature. |
| void FuelCellShop::Material::GasMixture::get_DChapmanEnskog_diffusion_coefficients_Dtemperature | ( | const std::vector< double > & | temperature, |
| std::vector< Table< 2, double > > & | dst | ||
| ) | const |
This function returns the first derivative 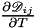 of the Maxwell-Stefan diffusion coefficients of gas
of the Maxwell-Stefan diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and variable temperature in the quadrature points of a mesh entity.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a constant total pressure and variable temperature in the quadrature points of a mesh entity.
| temperature | - temperature in the quadrature points of a mesh entity, |
| dst | - 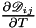 at a constant total pressure and variable temperature in the quadrature points of a mesh entity. at a constant total pressure and variable temperature in the quadrature points of a mesh entity. |
| const Table< 2, double > FuelCellShop::Material::GasMixture::get_DChapmanEnskog_diffusion_coefficients_Dtemperature | ( | const double & | total_pressure, |
| const double & | temperature | ||
| ) | const |
This function returns the first derivative 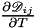 of the Maxwell-Stefan diffusion coefficients of gas
of the Maxwell-Stefan diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature.
| total_pressure | - total pressure, |
| temperature | - temperature. |
| void FuelCellShop::Material::GasMixture::get_DChapmanEnskog_diffusion_coefficients_Dtemperature | ( | const std::vector< double > & | total_pressure, |
| const std::vector< double > & | temperature, | ||
| std::vector< Table< 2, double > > & | dst | ||
| ) | const |
This function returns the first derivative 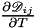 of the Maxwell-Stefan diffusion coefficients of gas
of the Maxwell-Stefan diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature in the quadrature points of a mesh entity.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable total pressure and temperature in the quadrature points of a mesh entity.
| total_pressure | - total pressure in the quadrature points of a mesh entity, |
| temperature | - temperature in the quadrature points of a mesh entity, |
| dst | - 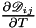 at a variable total pressure and temperature in the quadrature points of a mesh entity. at a variable total pressure and temperature in the quadrature points of a mesh entity. |
| const double FuelCellShop::Material::GasMixture::get_DChapmanEnskog_isobaric_diffusion_coefficient_Dtemperature | ( | const double & | temperature | ) | const |
This function returns the first derivative 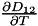 of the Maxwell-Stefan isobaric diffusion coefficient of gas
of the Maxwell-Stefan isobaric diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable temperature.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable temperature.
| temperature | - temperature. |
| void FuelCellShop::Material::GasMixture::get_DChapmanEnskog_isobaric_diffusion_coefficient_Dtemperature | ( | const std::vector< double > & | temperature, |
| std::vector< double > & | dst | ||
| ) | const |
This function returns the first derivative 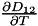 of the Maxwell-Stefan isobaric diffusion coefficient of gas
of the Maxwell-Stefan isobaric diffusion coefficient of gas  in gas
in gas  (or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable temperature in the quadrature points of a mesh entity.
(or vice-versa) written in the Chapman Enskog form (binary gas mixture only) at a variable temperature in the quadrature points of a mesh entity.
| temperature | - temperature in the quadrature points of a mesh entity, |
| dst | - 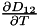 at a variable temperature in the quadrature points of a mesh entity. at a variable temperature in the quadrature points of a mesh entity. |
| const Table< 2, double > FuelCellShop::Material::GasMixture::get_DChapmanEnskog_isobaric_diffusion_coefficients_Dtemperature | ( | const double & | temperature | ) | const |
This function returns the first derivative 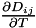 of the Maxwell-Stefan isobaric diffusion coefficients of gas
of the Maxwell-Stefan isobaric diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable temperature.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable temperature.
| temperature | - temperature. |
| void FuelCellShop::Material::GasMixture::get_DChapmanEnskog_isobaric_diffusion_coefficients_Dtemperature | ( | const std::vector< double > & | temperature, |
| std::vector< Table< 2, double > > & | dst | ||
| ) | const |
This function returns the first derivative 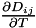 of the Maxwell-Stefan isobaric diffusion coefficients of gas
of the Maxwell-Stefan isobaric diffusion coefficients of gas  in gas
in gas  written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable temperature in the quadrature points of a mesh entity.
written in the Chapman Enskog form (ternary and more complicated gas mixtures) at a variable temperature in the quadrature points of a mesh entity.
| temperature | - temperature in the quadrature points of a mesh entity, |
| dst | - 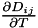 at a variable temperature in the quadrature points of a mesh entity. at a variable temperature in the quadrature points of a mesh entity. |
| void FuelCellShop::Material::GasMixture::get_delta_bulk_viscosity | ( | const std::vector< PureGas * > & | gases, |
| const std::vector< std::vector< std::vector< double > > > & | deltaPartialViscosity, | ||
| std::vector< std::vector< std::vector< double > > > & | deltaBulkViscosity | ||
| ) | const |
Loops through all variations of partial viscosity and calculates the varation in bulk viscosity according to bulk_viscosity_mode.
All vectors must be sized correctly before using this function.
|
inline |
Return gas stored in index ind.
References gases.
|
inline |
This function returns gases.
References gases.
| void FuelCellShop::Material::GasMixture::get_isothermal_nonisobaric_delta_partial_viscosity | ( | const double & | tempOfMixture, |
| const std::vector< std::vector< std::vector< double > > > & | paramMatrix, | ||
| const std::vector< FullMatrix< double > > & | PInv, | ||
| const std::vector< double > & | porosity, | ||
| const std::vector< double > & | molarMass, | ||
| const std::vector< double > & | dynamicViscosity, | ||
| const std::vector< double > & | collisionDiameter, | ||
| const std::vector< std::vector< std::vector< double > > > & | deltaDensity, | ||
| const std::vector< std::vector< double > > & | density, | ||
| std::vector< std::vector< std::vector< double > > > & | deltaPartialViscosity | ||
| ) | const |
This function calculates the variation in partial viscosity based on value stored in mixture_viscosity_mode and ASSUMES ISOTHERMAL and NONISOBARIC fluid flow.
Developers should call this function instead of directly calling Wilke, Omega, or Dynamic directly for the delta partial viscosity model. This function requires the following parameters:
| tempOfMixture | - temperature of the element [K], |
| paramMatrix | - this parameter provides a necessary matrix and is outputed by reference from get_partial_viscosity. This is done to decrease computations, |
| PInv | ( 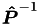 ) - calculated previously (numerically) and returned by get_partial_viscosity, ) - calculated previously (numerically) and returned by get_partial_viscosity, |
| porosity | - vector of quadrature points of porosity in element, |
| molarMass | - vector of molar masses of each species; [g/mol], |
| dynamicViscosity | - vector of dynamic viscosities of each species; [g/cm*s], |
| collisionDiameter | - vector of collision diameters of each species; [m], |
| deltaDensity | - variation of density in element (i.e. density[s][q][k], s=species, q=quadrature, k=dof); same unit standard as density, |
| density | - density in element (i.e. density[s][q], s=species, q=quadrature); [g/cm^3], |
| deltaPartialViscosity | - variation is partial viscosity returned by reference from function in element (i.e. deltaPartialViscosity[s][q][k], s=species, q=quadrature, k=dof). |
| std::vector<double> FuelCellShop::Material::GasMixture::get_isothermal_nonisobaric_OmegaKG_partial_viscosity | ( | const std::vector< double > & | density, |
| const std::vector< double > & | collisionDiameter, | ||
| const std::vector< double > & | molarMass, | ||
| const double & | temperature, | ||
| const double & | porosity | ||
| ) | const |
This is an overloaded function that calculates the Kerkhof and Geboers partial viscosity model based on the Omega integrals and ASSUMES ISOTHERMAL and NONISOBARIC fluid flow, but doesn't return the 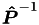 matrix or a table of the Omega integrals.
matrix or a table of the Omega integrals.
The equations for the OmegaKG partial viscosity model are:
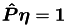 ,
,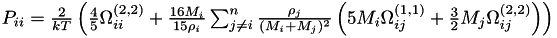 ,
,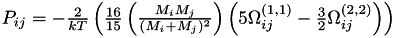 ,
,![$ \Omega_{ij}^{(\ell,s)} = \Omega_{ij}^{*(\ell,s)} \left[\Omega_{ij}^{(\ell,s)}\right]_{rs} $](form_633.png) ,
,![$ \left[Q_{ij}^{\ell}\right]_{rs} = \left( 1 - \frac{1}{2} \left( \frac{1+(-1)^\ell}{1+\ell}\right) \right)\pi \sigma_{ij}^2 $](form_634.png) ,
,![$ \left[\Omega_{ij}^{(\ell,s)}\right]_{rs} = \sqrt{\frac{kT}{2 \pi \mu_{ij}}} \left( \frac{(s+1)!}{2} \right) \left[Q_{ij}^{\ell}\right]_{rs} $](form_635.png) ,
,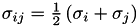 ,
,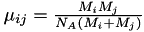
| density | ( 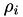 ) - density; [g/cm^3], ) - density; [g/cm^3], |
| collisionDiameter | ( 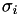 ) - collision diameter [m], ) - collision diameter [m], |
| molarMass | ( 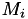 ) - molar mass [g/mol], ) - molar mass [g/mol], |
| temperature | ( 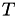 ) - temperature [K]. ) - temperature [K]. |
| porosity | ( 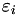 ) - porosity, ) - porosity, |
NOTE: that the global variable gases is used in this function. So set before functional call by using GasMixture object set_gases() function.
| std::vector<double> FuelCellShop::Material::GasMixture::get_isothermal_nonisobaric_OmegaKG_partial_viscosity | ( | const std::vector< double > & | density, |
| const std::vector< double > & | collisionDiameter, | ||
| const std::vector< double > & | molarMass, | ||
| const double & | temperature, | ||
| const double & | porosity, | ||
| std::vector< std::vector< double > > & | omegaIntegralTable, | ||
| FullMatrix< double > & | PInv | ||
| ) | const |
Same as other overloaded function (ASSUMES ISOTHERMAL and NONISOBARIC fluid flow).
The difference is that this one will return by reference 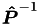 and you can specify a porosity. This is for convience if later calculations are needed so
and you can specify a porosity. This is for convience if later calculations are needed so 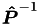 does not need to be re-computed (like when calculating the variation in the partial viscosity of the mixture). No need to size
does not need to be re-computed (like when calculating the variation in the partial viscosity of the mixture). No need to size 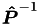 properly as all values are cleared at the beginning and then values pushed in after. The volume averaged OmegaKG partial viscosity model equations are:
properly as all values are cleared at the beginning and then values pushed in after. The volume averaged OmegaKG partial viscosity model equations are:
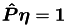 ,
,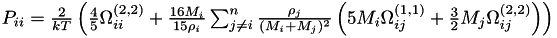 ,
,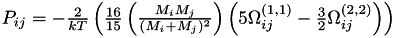 ,
,![$ \Omega_{ij}^{(\ell,s)} = \Omega_{ij}^{*(\ell,s)} \left[\Omega_{ij}^{(\ell,s)}\right]_{rs} $](form_633.png) ,
,![$ \left[Q_{ij}^{\ell}\right]_{rs} = \left( 1 - \frac{1}{2} \left( \frac{1+(-1)^\ell}{1+\ell}\right) \right)\pi \sigma_{ij}^2 $](form_634.png) ,
,![$ \left[\Omega_{ij}^{(\ell,s)}\right]_{rs} = \sqrt{\frac{kT}{2 \pi \mu_{ij}}} \left( \frac{(s+1)!}{2} \right) \left[Q_{ij}^{\ell}\right]_{rs} $](form_635.png) ,
,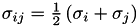 ,
,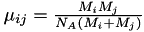
| density | ( 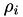 ) - phase average of density; [g/cm^3], ) - phase average of density; [g/cm^3], |
| collisionDiameter | ( 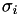 ) - collision diameter [m], ) - collision diameter [m], |
| molarMass | ( 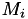 ) - molar mass [g/mol], ) - molar mass [g/mol], |
| temperature | ( 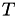 ) - temperature [K], ) - temperature [K], |
| porosity | ( 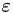 ) - porosity, ) - porosity, |
| omegaIntegralTable | - returned by reference to reduce computations when calculation variation. Contains a 2n x n matrix (n is species number) with the 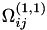 on top followed by on top followed by 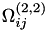 |
| PInv | ( 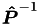 ) - returned by reference for possible later calculations (i.e. PInv[s1][s2], s1=species1, s2=species2). ) - returned by reference for possible later calculations (i.e. PInv[s1][s2], s1=species1, s2=species2). |
NOTE: that the global variable gases is used in this function. So set before functional call by using GasMixture object set_gases() function.
| const std::vector< std::vector<double> > FuelCellShop::Material::GasMixture::get_isothermal_nonisobaric_partial_viscosity | ( | const double & | tempOfMixture, |
| const std::vector< std::vector< double > > & | density, | ||
| const std::vector< double > & | molarMass, | ||
| const std::vector< double > & | dynamicViscosity, | ||
| const std::vector< double > & | collisionDiameter, | ||
| const std::vector< double > & | porosity, | ||
| std::vector< std::vector< std::vector< double > > > & | paramMatrix, | ||
| std::vector< FullMatrix< double > > & | PInv | ||
| ) | const |
This function calculates the partial viscosity based on value stored in mixture_viscosity_mode and ASSUMES ISOTHERMAL and NONISOBARIC fluid flow.
Developers should call this function instead of directly calling Wilke, OmegaKG, or Dynamic directly for the partial viscosity model. This function requires the following parameters:
| tempOfMixture | - temperature of the element; [K], |
| density | - density in element (i.e. density[s][q], s=species, q=quadrature); [g/cm^3], |
| molarMass | - vector of molar masses of each species; [g/mol], |
| dynamicViscosity | - vector of dynamic viscosities of each species; [g/cm*s], |
| collisionDiameter | - vector of collision diameters of each species; [m], |
| porosity | - vector of quadrature points of porosity in element, |
| paramMatrix | - this parameter provides a necessary matrix and is outputed by reference to be used for calculating the variation in partial viscosity. This is done to decrease computations, and used strictly internally, in get_delta_partial_viscosity(). Value is cleared and resized internally. Vector format is paramMatrix[q][s1][s2], q=quadrature, s1=species1, s2=species2, |
| PInv | - this parameter provides the inverse of P for the calculation of OmegaKG viscosity and variation of. |
NOTE: you have to set std::vector< NAME::PureGas* > gases in your GasMixture object to be the gases used, before calling this function
| std::vector<double> FuelCellShop::Material::GasMixture::get_isothermal_nonisobaric_Wilke_partial_viscosity | ( | const std::vector< double > & | density, |
| const std::vector< double > & | dynamicViscosity, | ||
| const std::vector< double > & | molarMass, | ||
| const double & | porosity | ||
| ) | const |
This is an overloaded function that calculates the Wilke partial viscosity model and ASSUMES ISOTHERMAL and NONISOBARIC fluid flow, but doesn't return the 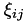 matrix.
matrix.
The Wilke partial viscosity model equations are:
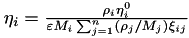 ,
,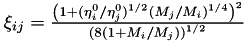
| density | ( 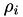 ) - density; [g/cm^3], ) - density; [g/cm^3], |
| dynamicViscosity | ( 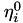 ) - dynamic viscosity [g/cm*s], ) - dynamic viscosity [g/cm*s], |
| molarMass | ( 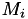 ) - molar mass [g/mol], ) - molar mass [g/mol], |
| porosixty | ( 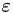 ) - porosity. ) - porosity. |
| std::vector<double> FuelCellShop::Material::GasMixture::get_isothermal_nonisobaric_Wilke_partial_viscosity | ( | const std::vector< double > & | density, |
| const std::vector< double > & | dynamicViscosity, | ||
| const std::vector< double > & | molarMass, | ||
| const double & | porosity, | ||
| std::vector< std::vector< double > > & | xi | ||
| ) | const |
Same as another overloaded function (ASSUMES ISOTHERMAL and NONISOBARIC fluid flow).
The difference is that this one will return by reference 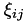 . This is for convience if later calculations are needed so
. This is for convience if later calculations are needed so 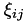 does not need to be re-computed (like when calculating the variation in the partial viscosity of the mixture). No need to size
does not need to be re-computed (like when calculating the variation in the partial viscosity of the mixture). No need to size 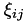 properly as all values are cleared at the beginning and then values pushed in after. The volume averaged Wilke partial viscosity model equations are:
properly as all values are cleared at the beginning and then values pushed in after. The volume averaged Wilke partial viscosity model equations are:
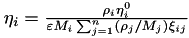 ,
,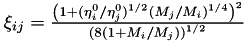
| density | ( 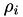 ) - phase average of density; [g/cm^3], ) - phase average of density; [g/cm^3], |
| dynamicViscosity | ( 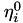 ) - dynamic viscosity [g/cm*s], ) - dynamic viscosity [g/cm*s], |
| molarMass | ( 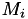 ) - molar mass [g/mol], ) - molar mass [g/mol], |
| porosity | ( 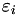 ) - porosity, ) - porosity, |
| xi | ( 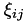 ) - returned by reference for possible later calculations (i.e. xi[s1][s2], s1=species1, s2=species2). ) - returned by reference for possible later calculations (i.e. xi[s1][s2], s1=species1, s2=species2). |
| void FuelCellShop::Material::GasMixture::get_nonisothermal_nonisobaric_delta_partial_viscosity | ( | const std::vector< double > & | temperature, |
| const std::vector< std::vector< std::vector< double > > > & | paramMatrix, | ||
| const std::vector< FullMatrix< double > > & | PInv, | ||
| const std::vector< double > & | porosity, | ||
| const std::vector< double > & | molarMass, | ||
| const std::vector< std::vector< double > > & | dynamicViscosity, | ||
| const std::vector< double > & | collisionDiameter, | ||
| const std::vector< std::vector< std::vector< double > > > & | deltaDensity, | ||
| const std::vector< std::vector< double > > & | density, | ||
| std::vector< std::vector< std::vector< double > > > & | deltaPartialViscosity | ||
| ) | const |
This function calculates the variation in partial viscosity based on value stored in mixture_viscosity_mode and ASSUMES NONISOTHERMAL and NONISOBARIC fluid flow.
Developers should call this function instead of directly calling Wilke, Omega, or Dynamic directly for the delta partial viscosity model. This function requires the following parameters:
| temperature | - temperature of the element (i.e. temperature[q], q=quadrature); [K], |
| paramMatrix | - this parameter provides a necessary matrix and is outputed by reference from get_partial_viscosity. This is done to decrease computations, |
| PInv | ( 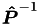 ) - calculated previously (numerically) and returned by get_partial_viscosity, ) - calculated previously (numerically) and returned by get_partial_viscosity, |
| porosity | - vector of quadrature points of porosity in element, |
| molarMass | - vector of molar masses of each species; [g/mol], |
| dynamicViscosity | - vector of dynamic viscosities of each species (i.e. dynamicViscosity[s][q], s=species, q=quadrature); [g/cm*s], |
| collisionDiameter | - vector of collision diameters of each species; [m], |
| deltaDensity | - variation of density in element (i.e. density[s][q][k], s=species, q=quadrature, k=dof); same unit standard as density, |
| density | - density in element (i.e. density[s][q], s=species, q=quadrature); [g/cm^3], |
| deltaPartialViscosity | - variation is partial viscosity returned by reference from function in element (i.e. deltaPartialViscosity[s][q][k], s=species, q=quadrature, k=dof). |
| std::vector<double> FuelCellShop::Material::GasMixture::get_nonisothermal_nonisobaric_OmegaKG_partial_viscosity | ( | const std::vector< double > & | density, |
| const std::vector< double > & | collisionDiameter, | ||
| const std::vector< double > & | molarMass, | ||
| const double & | temperature, | ||
| const double & | porosity, | ||
| std::vector< std::vector< double > > & | omegaIntegralTable, | ||
| FullMatrix< double > & | PInv | ||
| ) | const |
This function calculates the partial viscosity using the OmegaKG model based on value stored in mixture_viscosity_mode and ASSUMES NONISOTHERMAL and NONISOBARIC fluid flow.
| const std::vector< std::vector<double> > FuelCellShop::Material::GasMixture::get_nonisothermal_nonisobaric_partial_viscosity | ( | const std::vector< double > & | temperature, |
| const std::vector< std::vector< double > > & | density, | ||
| const std::vector< double > & | molarMass, | ||
| const std::vector< std::vector< double > > & | dynamicViscosity, | ||
| const std::vector< double > & | collisionDiameter, | ||
| const std::vector< double > & | porosity, | ||
| std::vector< std::vector< std::vector< double > > > & | paramMatrix, | ||
| std::vector< FullMatrix< double > > & | PInv | ||
| ) | const |
This function calculates the partial viscosity based on value stored in mixture_viscosity_mode and ASSUMES NONISOTHERMAL and NONISOBARIC fluid flow.
Developers should call this function instead of directly calling Wilke, OmegaKG, or Dynamic directly for the partial viscosity model. This function requires the following parameters:
| temperature | - temperature in element (i.e. temperature[q], q=quadrature); [K], |
| density | - density in element (i.e. density[s][q], s=species, q=quadrature); [g/cm^3], |
| molarMass | - vector of molar masses of each species; [g/mol], |
| dynamicViscosity | - dynamic viscosities of element (i.e. dynamicViscosity[s][q], s=species, q=quadrature); [g/cm*s], |
| collisionDiameter | - vector of collision diameters of each species; [m], |
| porosity | - vector of quadrature points of porosity in element, |
| paramMatrix | - this parameter provides a necessary matrix and is outputed by reference to be used for calculating the variation in partial viscosity. This is done to decrease computations, and used strictly internally, in get_delta_partial_viscosity(). Value is cleared and resized internally. Vector format is paramMatrix[q][s1][s2], q=quadrature, s1=species1, s2=species2, |
| PInv | - this parameter provides the inverse of P for the calculation of OmegaKG viscosity and variation of. |
NOTE: you have to set std::vector< NAME::PureGas* > gases in your GasMixture object to be the gases used, before calling this function
| std::vector<double> FuelCellShop::Material::GasMixture::get_nonisothermal_nonisobaric_Wilke_partial_viscosity | ( | const std::vector< double > & | density, |
| const std::vector< double > & | dynamicViscosity, | ||
| const std::vector< double > & | molarMass, | ||
| const double & | porosity, | ||
| std::vector< std::vector< double > > & | xi | ||
| ) | const |
This function calculates the partial viscosity using the Wilke model based on value stored in mixture_viscosity_mode and ASSUMES NONISOTHERMAL and NONISOBARIC fluid flow.
| void FuelCellShop::Material::GasMixture::get_Null_delta_viscosity | ( | std::vector< std::vector< std::vector< double > > > & | deltaViscosity | ) | const |
Returns a std::vector< std::vector< std::vector<double> > > of 0s.
This is used for the dynamic viscosity partial viscosity model as it is not a function of density or velocity. As such, the variation is 0. Note that deltaViscosity must be properly sized before sending to this function.
|
protected |
This function returns 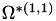 integral at a variable temperature.
integral at a variable temperature.
This equation is only valid in range 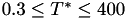 and empirical constants were taken from "Toward a Unified Theory of Isotropic Molecular Transport Phenomena" by Kerkhof and Geboers, which used Table C2 from the data in "Molecular Theory of Gases and Liquids" by Hirschfelder.
and empirical constants were taken from "Toward a Unified Theory of Isotropic Molecular Transport Phenomena" by Kerkhof and Geboers, which used Table C2 from the data in "Molecular Theory of Gases and Liquids" by Hirschfelder.
| temperature | - temperature [K], |
| N1 | - number of the first gas from gases, |
| N2 | - number of the second gas from gases. |
|
protected |
This function returns 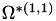 integral at a variable temperature in the quadrature points of a mesh entity.
integral at a variable temperature in the quadrature points of a mesh entity.
this equation is only valid in range 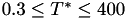 and empirical constants were taken from "Toward a Unified Theory of Isotropic Molecular Transport Phenomena" by Kerkhof and Geboers, which used Table C2 from the data in "Molecular Theory of Gases and Liquids" by Hirschfelder.
and empirical constants were taken from "Toward a Unified Theory of Isotropic Molecular Transport Phenomena" by Kerkhof and Geboers, which used Table C2 from the data in "Molecular Theory of Gases and Liquids" by Hirschfelder.
| temperature | - temperature in the quadrature points of a mesh entity [K], |
| omega_integral | - 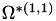 integral at a variable temperature in the quadrature points of a mesh entity, integral at a variable temperature in the quadrature points of a mesh entity, |
| N1 | - index of the first gas from gases, |
| N2 | - index of the second gas from gases. |
|
protected |
This function returns 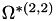 integral at a variable temperature.
integral at a variable temperature.
this equation is only valid in range 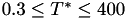 and empirical constants were taken from "Toward a Unified Theory of Isotropic Molecular Transport Phenomena" by Kerkhof and Geboers, which used Table C2 from the data in "Molecular Theory of Gases and Liquids" by Hirschfelder.
and empirical constants were taken from "Toward a Unified Theory of Isotropic Molecular Transport Phenomena" by Kerkhof and Geboers, which used Table C2 from the data in "Molecular Theory of Gases and Liquids" by Hirschfelder.
| temperature | - temperature [K], |
| N1 | - number of the first gas from gases, |
| N2 | - number of the second gas from gases. |
|
protected |
This function returns 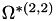 integral at a variable temperature in the quadrature points of a mesh entity.
integral at a variable temperature in the quadrature points of a mesh entity.
this equation is only valid in range 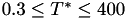 and empirical constants were taken from "Toward a Unified Theory of Isotropic Molecular Transport Phenomena" by Kerkhof and Geboers, which used Table C2 from the data in "Molecular Theory of Gases and Liquids" by Hirschfelder.
and empirical constants were taken from "Toward a Unified Theory of Isotropic Molecular Transport Phenomena" by Kerkhof and Geboers, which used Table C2 from the data in "Molecular Theory of Gases and Liquids" by Hirschfelder.
| temperature | - temperature in the quadrature points of a mesh entity [K], |
| omega_integral | - 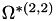 integral at a variable temperature in the quadrature points of a mesh entity, integral at a variable temperature in the quadrature points of a mesh entity, |
| N1 | - index of the first gas from gases, |
| N2 | - index of the second gas from gases. |
| void FuelCellShop::Material::GasMixture::get_OmegaKG_delta_partial_viscosity_wrt_density | ( | const double & | tempOfMixture, |
| const std::vector< std::vector< std::vector< double > > > & | omegaIntegralTable, | ||
| const std::vector< FullMatrix< double > > & | PInv, | ||
| const std::vector< double > & | porosity, | ||
| const std::vector< double > & | molarMass, | ||
| const std::vector< double > & | collisionDiameter, | ||
| const std::vector< std::vector< std::vector< double > > > & | deltaDensity, | ||
| const std::vector< std::vector< double > > & | density, | ||
| std::vector< std::vector< std::vector< double > > > & | deltaPartialViscosity | ||
| ) | const |
Calculates the variation in Kerkhof and Geboers partial viscosity model using Omega integrals w.r.t.
density ( 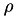 ). The equations are:
). The equations are:
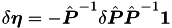 ,
,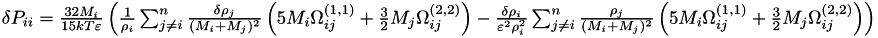 ,
,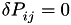 .
.| tempOfMixture | ( 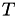 ) - temperature of the element [K], ) - temperature of the element [K], |
| omegaIntegralTable | - returned by reference to reduce computations when calculation variation. Contains a 2n x n matrix (n is species number) with the 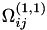 on top followed by on top followed by 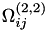 ; (i.e. omegaIntegralTable[q][s1][s2], q=quadrature, s1=species1, s2=species2). ; (i.e. omegaIntegralTable[q][s1][s2], q=quadrature, s1=species1, s2=species2). |
| PInv | ( 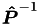 ) - calculated previously (numerically) and returned by get_partial_viscosity, ) - calculated previously (numerically) and returned by get_partial_viscosity, |
| porosity | ( 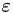 ) - porosity, ) - porosity, |
| molarMass | ( 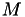 ) - vector of molar masses of each species; [g/mol], ) - vector of molar masses of each species; [g/mol], |
| collisionDiameter | ( 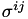 ) - vector of collision diameters of each species; [m], ) - vector of collision diameters of each species; [m], |
| deltaDensity | ( 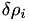 ) - varation in phase average of density; same unit standard as density, ) - varation in phase average of density; same unit standard as density, |
| density | ( 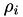 ) - phase average of density; [g/cm^3], ) - phase average of density; [g/cm^3], |
| deltaPartialViscosity | ( 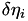 ) - variation is partial viscosity returned by reference from function in element (i.e. deltaPartialViscosity[s][q][k], s=species, q=quadrature, k=dof). ) - variation is partial viscosity returned by reference from function in element (i.e. deltaPartialViscosity[s][q][k], s=species, q=quadrature, k=dof). |
| void FuelCellShop::Material::GasMixture::get_OmegaKG_delta_partial_viscosity_wrt_temperature | ( | const std::vector< double > & | temperature, |
| const std::vector< std::vector< std::vector< double > > > & | omegaIntegralTable, | ||
| const std::vector< FullMatrix< double > > & | PInv, | ||
| const std::vector< double > & | porosity, | ||
| const std::vector< double > & | molarMass, | ||
| const std::vector< double > & | collisionDiameter, | ||
| const std::vector< std::vector< std::vector< double > > > & | deltaDensity, | ||
| const std::vector< std::vector< double > > & | density, | ||
| std::vector< std::vector< std::vector< double > > > & | deltaPartialViscosity | ||
| ) | const |
Calculates the variation in Kerkhof and Geboers partial viscosity model using Omega integrals w.r.t.
temperature ( 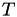 ). The equations are:
). The equations are:
NOTE: these equations are not volume averaged, which will need to be done.
| temperature | ( 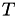 ) - temperature of the element [K], ) - temperature of the element [K], |
| omegaIntegralTable | - returned by reference to reduce computations when calculation variation. Contains a 2n x n matrix (n is species number) with the 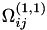 on top followed by on top followed by 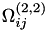 ; (i.e. omegaIntegralTable[q][s1][s2], q=quadrature, s1=species1, s2=species2). ; (i.e. omegaIntegralTable[q][s1][s2], q=quadrature, s1=species1, s2=species2). |
| PInv | ( 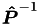 ) - calculated previously (numerically) and returned by get_partial_viscosity, ) - calculated previously (numerically) and returned by get_partial_viscosity, |
| porosity | ( 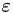 ) - porosity, ) - porosity, |
| molarMass | ( 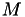 ) - vector of molar masses of each species; [g/mol], ) - vector of molar masses of each species; [g/mol], |
| collisionDiameter | ( 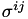 ) - vector of collision diameters of each species; [m], ) - vector of collision diameters of each species; [m], |
| deltaDensity | ( 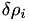 ) - varation in phase average of density; same unit standard as density, ) - varation in phase average of density; same unit standard as density, |
| density | ( 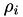 ) - phase average of density; [g/cm^3], ) - phase average of density; [g/cm^3], |
| deltaPartialViscosity | ( 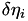 ) - variation is partial viscosity returned by reference from function in element (i.e. deltaPartialViscosity[s][q][k], s=species, q=quadrature, k=dof). ) - variation is partial viscosity returned by reference from function in element (i.e. deltaPartialViscosity[s][q][k], s=species, q=quadrature, k=dof). |
|
inline |
This function returns temperature.
References temperature.
|
inline |
This function returns total_pressure.
References total_pressure.
| void FuelCellShop::Material::GasMixture::get_Wilke_delta_partial_viscosity_wrt_density | ( | const std::vector< std::vector< std::vector< double > > > & | xi, |
| const std::vector< double > & | porosity, | ||
| const std::vector< double > & | molarMass, | ||
| const std::vector< double > & | dynamicViscosity, | ||
| const std::vector< std::vector< std::vector< double > > > & | deltaDensity, | ||
| const std::vector< std::vector< double > > & | density, | ||
| std::vector< std::vector< std::vector< double > > > & | deltaPartialViscosity | ||
| ) | const |
Calculates the variation in Wilke's partial viscosity model w.r.t.
density ( 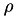 ). The equation it solves is:
). The equation it solves is:
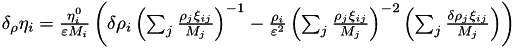
| xi | ( 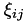 ) - calculated previously and returned by get_partial_viscosity, ) - calculated previously and returned by get_partial_viscosity, |
| porosity | ( 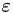 ) - porosity, ) - porosity, |
| molarMass | ( 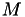 ) - vector of molar masses of each species; [g/mol], ) - vector of molar masses of each species; [g/mol], |
| dynamicViscosity | ( 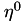 ) - vector of dynamic viscosities of each species; [g/cm*s], ) - vector of dynamic viscosities of each species; [g/cm*s], |
| deltaDensity | ( 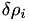 ) - varation in phase average of density; same unit standard as density, ) - varation in phase average of density; same unit standard as density, |
| density | ( 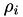 ) - phase average of density; [g/cm^3], ) - phase average of density; [g/cm^3], |
| deltaPartialViscosity | ( 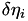 ) - variation is partial viscosity returned by reference from function in element (i.e. deltaPartialViscosity[s][q][k], s=species, q=quadrature, k=dof). ) - variation is partial viscosity returned by reference from function in element (i.e. deltaPartialViscosity[s][q][k], s=species, q=quadrature, k=dof). |
| void FuelCellShop::Material::GasMixture::get_Wilke_delta_partial_viscosity_wrt_temperature | ( | const std::vector< std::vector< std::vector< double > > > & | xi, |
| const std::vector< double > & | porosity, | ||
| const std::vector< double > & | molarMass, | ||
| const std::vector< double > & | dynamicViscosity, | ||
| const std::vector< std::vector< std::vector< double > > > & | deltaTemperature, | ||
| const std::vector< std::vector< double > > & | density, | ||
| std::vector< std::vector< std::vector< double > > > & | deltaPartialViscosity | ||
| ) | const |
Calculates the variation in Wilke's partial viscosity model w.r.t.
temperature ( 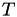 ). The equation it solves is:
). The equation it solves is:
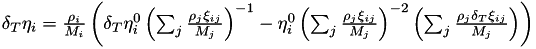
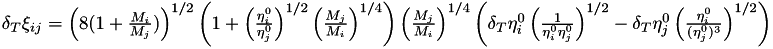
NOTE: these equations are not volume averaged, which will need to be done.
| xi | ( 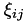 ) - calculated previously and returned by get_partial_viscosity, ) - calculated previously and returned by get_partial_viscosity, |
| porosity | ( 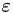 ) - porosity, ) - porosity, |
| molarMass | ( 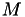 ) - vector of molar masses of each species; [g/mol], ) - vector of molar masses of each species; [g/mol], |
| dynamicViscosity | ( 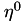 ) - vector of dynamic viscosities of each species; [g/cm*s], ) - vector of dynamic viscosities of each species; [g/cm*s], |
| deltaTemperature | ( 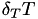 ) - varation in phase average of temperature; same unit standard as temperature, ) - varation in phase average of temperature; same unit standard as temperature, |
| density | ( 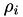 ) - phase average of density; [g/cm^3], ) - phase average of density; [g/cm^3], |
| deltaPartialViscosity | ( 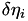 ) - variation is partial viscosity returned by reference from function in element (i.e. deltaPartialViscosity[s][q][k], s=species, q=quadrature, k=dof). ) - variation is partial viscosity returned by reference from function in element (i.e. deltaPartialViscosity[s][q][k], s=species, q=quadrature, k=dof). |
|
virtual |
Initialize parameters.
Reimplemented from FuelCellShop::Material::BaseMaterial.
|
inline |
Function returning the number of gases in the mixture.
References gases.
|
virtual |
This function prints out the material properties.
Reimplemented from FuelCellShop::Material::BaseMaterial.
|
inline |
This function sets gases.
References gases.
|
inline |
This function takes a temperature (K) and if Isothermal fluid flow is set to true in the data file then the inputted temperature will be used else the DUMMY value is used.
References temperature.
Referenced by FuelCell::OperatingConditions::set_gas_mixtures().

|
inline |
This function takes a pressure (Pa) and if Isobaric fluid flow is set to true in the data file then the inputted pressure will be used else the DUMMY value is used.
References total_pressure.
Referenced by FuelCell::OperatingConditions::set_gas_mixtures().

|
protected |
This std::vector contains all pure gases which form the whole gas mixture of a problem at hand.
Referenced by get_gas(), get_gases(), n_gases(), and set_gases().
|
protected |
| mixture_viscosity_mode=Wilke | - Wilke's formula for partial viscosity of each species is used, |
| mixture_viscosity_mode=OmegaKG | - Kerkhof and Geboers formula for partial viscosity of each species, using the Omega integrals, is used, |
| mixture_viscosity_mode=Dynamic | - The dynamic viscosity of each species is used as calculated by dynamic_viscosity_mode. |
|
protected |
This bool tells GasMisture if it should use isobaric assumption.
|
protected |
Temperature of the whole gas mixture, ![$ T \quad \left[ \text{K} \right] $](form_328.png) .
.
Referenced by get_temperature(), and set_temperature().
|
protected |
This bool tells GasMisture if it should use isothermal assumption.
|
protected |
Total pressure of the whole mixture, ![$ p_{\text{total}} \quad \left[ \text{Pa} \right] $](form_327.png) .
.
Referenced by get_total_pressure(), and set_total_pressure().
 1.8.5
1.8.5