|
OpenFCST: The open-source Fuel Cell Simulation Toolbox
|
|
OpenFCST: The open-source Fuel Cell Simulation Toolbox
|
Application class performing Newton's iteration. More...
#include <newton_w_3pp.h>
Public Member Functions | |
| Newton3pp (ApplicationBase &app) | |
| Constructor. More... | |
| void | declare_parameters (ParameterHandler ¶m) |
| Declare any additional parameters necessary for the solver. More... | |
| void | initialize (ParameterHandler ¶m) |
| Initialize NewtonBase and any additional parameters. More... | |
| virtual void | solve (FuelCell::ApplicationCore::FEVector &u, const FuelCell::ApplicationCore::FEVectors &in_vectors) |
| The actual Newton solver. More... | |
 Public Member Functions inherited from FuelCell::ApplicationCore::newtonBase Public Member Functions inherited from FuelCell::ApplicationCore::newtonBase | |
| newtonBase (ApplicationBase &app) | |
| Constructor, receiving the application computing the residual and solving the linear problem. More... | |
| void | _initialize (ParameterHandler ¶m) |
| Read the parameters local to newtonBase. More... | |
| double | threshold (double new_value) |
| Set the maximal residual reduction allowed without triggering assembling in the next step. More... | |
| void | initialize_initial_guess (BlockVector< double > &dst) |
| Control object for the Newton iteration. More... | |
| virtual void | assemble () |
| Instead of assembling, this function only sets a flag, such that the inner application will be required to assemble a new derivative matrix next time solve() is called. More... | |
| virtual double | residual (FuelCell::ApplicationCore::FEVector &dst, const FuelCell::ApplicationCore::FEVectors &rhs) |
| Returns the L2-norm of the residual and the residual vector in "dst" using the residual function in the ApplicationBase used to initialize the application. More... | |
 Public Member Functions inherited from FuelCell::ApplicationCore::ApplicationWrapper Public Member Functions inherited from FuelCell::ApplicationCore::ApplicationWrapper | |
| ApplicationWrapper (ApplicationBase &app) | |
| Constructor for a derived application. More... | |
| ~ApplicationWrapper () | |
| Destructor. More... | |
| virtual void | remesh () |
| Generate the next mesh depending on the mesh generation parameters. More... | |
| virtual void | init_vector (FEVector &dst) const |
| Initialize vector to problem size. More... | |
| virtual double | residual (FEVector &dst, const FEVectors &src, bool apply_boundaries=true) |
Compute residual of src and store it into dst. More... | |
| virtual void | Tsolve (FEVector &dst, const FEVectors &src) |
Solve the dual system assembled with right hand side rhs and return the result in start. More... | |
| virtual double | estimate (const FEVectors &src) |
| Estimate cell-wise errors. More... | |
| virtual double | evaluate (const FEVectors &src) |
| Evaluate a functional. More... | |
| virtual void | grid_out (const std::string &filename) const |
| virtual void | data_out (const std::string &filename, const FEVectors &src) |
| Write data in the format specified by the ParameterHandler. More... | |
| virtual std::string | id () const |
| Return a unique identification string for this application. More... | |
| virtual void | notify (const Event &reason) |
| Add a reason for assembling. More... | |
 Public Member Functions inherited from FuelCell::ApplicationCore::ApplicationBase Public Member Functions inherited from FuelCell::ApplicationCore::ApplicationBase | |
| ApplicationBase (boost::shared_ptr< ApplicationData > data=boost::shared_ptr< ApplicationData >()) | |
| Constructor for an application. More... | |
| ApplicationBase (const ApplicationBase &other) | |
| Copy constructor. More... | |
| virtual | ~ApplicationBase () |
| Virtual destructor. More... | |
| void | print_parameters_to_file (ParameterHandler ¶m, const std::string &file_name, const ParameterHandler::OutputStyle &style) |
| Print default parameters for the application to a file. More... | |
| virtual void | start_vector (FEVector &dst, std::string) const |
| Initialize vector to problem size. More... | |
| virtual void | grid_out (const std::string &) |
| Write the mesh in the format specified by the ParameterHandler. More... | |
| boost::shared_ptr < ApplicationData > | get_data () |
| Get access to the protected variable data. More... | |
| const boost::shared_ptr < ApplicationData > | get_data () const |
| Get read-only access to the protected variable data. More... | |
| virtual void | clear () |
All true in notifications. More... | |
| virtual void | clear_events () |
All false in notifications. More... | |
| virtual unsigned int | get_solution_index () |
| Returns solution index. More... | |
Static Public Attributes | |
| static const FuelCell::ApplicationCore::Event | bad_derivative |
 Static Public Attributes inherited from FuelCell::ApplicationCore::newtonBase Static Public Attributes inherited from FuelCell::ApplicationCore::newtonBase | |
| static const FuelCell::ApplicationCore::Event | bad_derivative |
| The Event set if convergence is becoming bad and a new matrix should be assembled. More... | |
Private Member Functions | |
| void | set_predefined_parameters () |
| Define default parameters for convergence. More... | |
| double | sum_of_squares (double residual_norm) |
| Sum of squares. More... | |
| double | three_point_step (int line_search_iterations, double lambda_current, double lambda_previous, double mf_original, double mf_current, double mf_previous) |
| Merit Function. More... | |
| bool | armijo (double step_length, double residual_norm, double new_residual_norm) |
| Determines step size by three point parabolic function. More... | |
Private Attributes | |
| double | max_reduction_factor |
| Convergance criterion. More... | |
| double | min_reduction_factor |
min_reduction_factor corresponds to 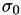 More... More... | |
| double | alpha |
| This parameter is used in order to assess when the line search should be stopped. More... | |
| bool | with_prediction |
| Boolean variable that specifies if the three-point method is used with (true) or without (false) prediction, i.e. More... | |
| bool | use_predefined |
| Flag so that predefined parameters are used. More... | |
Additional Inherited Members | |
 Public Attributes inherited from FuelCell::ApplicationCore::newtonBase Public Attributes inherited from FuelCell::ApplicationCore::newtonBase | |
| ReductionControl | control |
| Control object for the Newton iteration. More... | |
| double | numIter |
| Number of Iterations;. More... | |
 Protected Member Functions inherited from FuelCell::ApplicationCore::newtonBase Protected Member Functions inherited from FuelCell::ApplicationCore::newtonBase | |
| void | debug_output (const FEVector &sol, const FEVector &update, const FEVector &residual) const |
| Function used to output any necessary information at each Newton iteration for debugging purposes. More... | |
 Protected Member Functions inherited from FuelCell::ApplicationCore::ApplicationWrapper Protected Member Functions inherited from FuelCell::ApplicationCore::ApplicationWrapper | |
| SmartPointer< ApplicationBase > | get_wrapped_application () |
| Gain access to the inner application. More... | |
 Protected Member Functions inherited from FuelCell::ApplicationCore::ApplicationBase Protected Member Functions inherited from FuelCell::ApplicationCore::ApplicationBase | |
| void | print_caller_name (const std::string &caller_name) const |
| Print caller name. More... | |
 Protected Attributes inherited from FuelCell::ApplicationCore::newtonBase Protected Attributes inherited from FuelCell::ApplicationCore::newtonBase | |
| bool | assemble_now |
| This flag is set by the function assemble(), indicating that the matrix must be assembled anew upon start. More... | |
| double | assemble_threshold |
| Threshold for re-assembling matrix. More... | |
| bool | debug_solution |
Print updated solution after each step into file Newton_uNNN? More... | |
| bool | debug_update |
Print Newton update after each step into file Newton_dNNN? More... | |
| bool | debug_residual |
Print Newton residual after each step into file Newton_rNNN? More... | |
| unsigned int | debug |
| Write debug output to FcstUtilities::log; the higher the number, the more output. More... | |
| unsigned int | step |
| The number of a basic Newton iteration. More... | |
| std::vector< unsigned int > | blocks |
| This vector specifies the blocks of the global solution which are supposed to be treated specially. More... | |
| unsigned int | n_blocks |
The total number of blocks. More... | |
 Protected Attributes inherited from FuelCell::ApplicationCore::ApplicationWrapper Protected Attributes inherited from FuelCell::ApplicationCore::ApplicationWrapper | |
| SmartPointer< ApplicationBase > | app |
| Pointer to the application this one depends upon. More... | |
 Protected Attributes inherited from FuelCell::ApplicationCore::ApplicationBase Protected Attributes inherited from FuelCell::ApplicationCore::ApplicationBase | |
| boost::shared_ptr < ApplicationData > | data |
| Object for auxiliary data. More... | |
| Event | notifications |
| Accumulate reasons for assembling here. More... | |
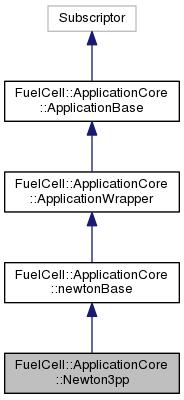
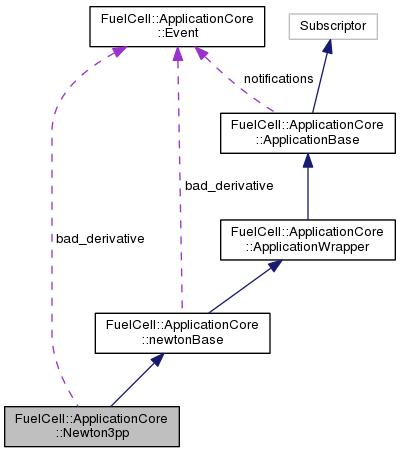
Application class performing Newton's iteration.
At each iteration a line search is performed using a three point parabolic algorithm to enhance robustness of the algorithm and to improve convergence to a global solution. Either a standard three point parabolic algorithm or a three point parabolic algorithm with prediction can be used depending on the input parameter "set Include step size prediction" in the Newton section of the input file. If this option is set to true, the algorithm with prediction is used. Othewise, the algorithm without prediction is used.
The three-point parabolic model, described in section 8.3.1 of [1], attempts to find a step size length, 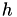 , such that it minimizes the scalar function
, such that it minimizes the scalar function
![\[ f (h) = \| \mathbf{F}(\mathbf{x}_{i−1} + h \delta \mathbf{x} ) \|_2^2. \]](form_528.png)
where the meaning of 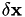 and how it is obtain is described in the documentation for the base class, i.e. newtonBase.
and how it is obtain is described in the documentation for the base class, i.e. newtonBase.
We estimate the norm above using the following three-point interpolating polynomial
![\[ p(h) = f (h) = f(0) + \frac{h}{h_{j-1} − h_{j−2}} \left( \frac{(h − h_{j−2}) ( f(h_{j−1}) − f(0) )}{h_{j−1}} + \frac{(h_{j−1} − h)(f(h_{j−2})-f(0)}{h_{j−2}} \right ) \]](form_529.png)
where 0, 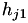 ,
, 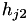 are the initial and the two lastly rejected step sizes in the interpolation.
are the initial and the two lastly rejected step sizes in the interpolation.
Using the equation above, and assuming that 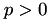 , the step size
, the step size 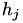 is given by
is given by
![\[ h_j = − \frac{p'(0)}{p''(0)} \]](form_533.png)
If 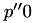 ,
, 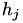 is reduced by a fixed amount.
is reduced by a fixed amount.
The three-point parabolic method is continued until a sufficient decrease in the residual 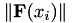 occurs based on the condition
occurs based on the condition
![\[ \| \mathbf{F}(\mathbf{x_{i−1}} + h_j \delta \mathbf{x}) \| < (1 − \alpha h_j ) \| \mathbf{F}(x_{i−1}) \|. \]](form_536.png)
where ![$ \alpha ∈ [0, 1] $](form_537.png) . In practice,
. In practice, 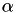 is typically
is typically 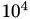 [2].
[2].
When implementing this method, there are a few considerations to take into account.
To prevent a reduction in the step size that is either too large or too small to be effective, we allow the user to specify a maximum and minimum reduction rate, i.e. 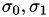 . Therefore,
. Therefore, 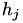 must equal
must equal 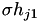 , where
, where ![$ \sigma ∈ [ \sigma_0 , \sigma_1] $](form_542.png) . This is guaranteed by making the following check after
. This is guaranteed by making the following check after 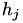 is determined
is determined
![\[ h_j = \left\{ \begin{array}{ll} \sigma_0 h_{j−1} & \mbox{ if } h_j < \sigma_0 h_{j−1} \\ \sigma_1 h_{j−1} & \mbox{ if } h_j > \sigma_1 h_{j−1} \\ h_j & \mbox{otherwise}. \end{array} \right. \]](form_543.png)
The three-point interpolating polynomial also requires some initial values for 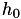 and
and 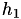 . If a maximum reduction factor is set, then it is convenient to choose
. If a maximum reduction factor is set, then it is convenient to choose
![\[ h_0 = 1, h_1 = \sigma_1 \]](form_546.png)
The value of 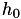 can be seen as an initial guess for the three-point parabolic method. In the previous section, we simply set
can be seen as an initial guess for the three-point parabolic method. In the previous section, we simply set 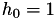 . Of course, it is very likely that 1 is a poor choice for the initial guess. This results in additional line-search iterations.
. Of course, it is very likely that 1 is a poor choice for the initial guess. This results in additional line-search iterations.
In an effort to reduce the number of line-search iterations, we can use the previous step size to more accurately choose an initial step size 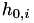 for the current Newton iteration
for the current Newton iteration  . However, there is also a possibility that the previous step size is a poor choice for an initial guess, therefore we use the condition
. However, there is also a possibility that the previous step size is a poor choice for an initial guess, therefore we use the condition
![\[ h_{0,i} = \left\{ \begin{array}{ll} h_{i−1} & \mbox{ if } h_{i-1} < h_{i−2}(1-\alpha) \\ min(1, 2 h_{i-1}) & \mbox{otherwise}. \end{array} \right. \]](form_549.png)
The step sizes 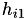 and
and 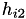 are from previous two Newton iterations. Initially,
are from previous two Newton iterations. Initially, 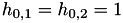 .
.
Using this strategy results in a predictor-corrector approach to the three-point parabolic method. The condition above predicts the value of the step size. After, the three-point parabolic method simply corrects for the differences between 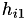 and
and 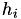 .
.
The parameters that control all Newton solvers are defined in the subsection Newton in the data input file. The parameters are the following:
[1] C. T. Kelley. Iterative methods for linear and nonlinear equations, volume 16 of Frontiers in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 1995. With separately available software.
[2] C. T. Kelley. Solving nonlinear equations with Newton’s method. Fundamentals of Algorithms. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 2003.
| FuelCell::ApplicationCore::Newton3pp::Newton3pp | ( | ApplicationBase & | app | ) |
Constructor.
|
private |
Determines step size by three point parabolic function.
|
virtual |
Declare any additional parameters necessary for the solver.
In this case the only additional parameter is a bool parameter estating if we want to use a Newton step prediction, i.e.
In subsection Newton you have the following option:
If true then a three-point parabolic method with prediction is used. Otherwise, the standard three-point parabolic is used.
Reimplemented from FuelCell::ApplicationCore::newtonBase.
|
virtual |
Initialize NewtonBase and any additional parameters.
Reimplemented from FuelCell::ApplicationCore::newtonBase.
|
inlineprivate |
Define default parameters for convergence.
These depend on refinement level.
References alpha, FuelCell::ApplicationCore::ApplicationBase::get_data(), max_reduction_factor, and min_reduction_factor.

|
virtual |
The actual Newton solver.
In this section, the Newton solver performs the iterations necessary to solve the nonlinear system. During the process it will call assemble() and residual() as needed. Once it is done, it will return the solution as parameter {u}.
Implements FuelCell::ApplicationCore::newtonBase.
|
private |
Sum of squares.
|
private |
Merit Function.
|
private |
This parameter is used in order to assess when the line search should be stopped.
This value should be between zero and one. In practice, 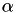 is typically
is typically 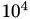 .
.
The larger the value of 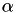 , the strictest the convergence criteria, i.e.
, the strictest the convergence criteria, i.e.
![\[ \| \mathbf{F}(\mathbf{x_{i−1}} + h_j \delta \mathbf{x}) \| < (1 − \alpha h_j ) \| \mathbf{F}(x_{i−1}) \|. \]](form_536.png)
will be.
This value can be modified in the input file in subsection Newton using "set alpha = 1e-4".
Referenced by set_predefined_parameters().
|
static |
|
private |
Convergance criterion.
To prevent a reduction in the step size that is either too large or too small to be effective, we allow the user to specify a maximum and minimum reduction rate, i.e. 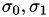 . Therefore,
. Therefore, 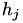 must equal
must equal 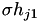 , where
, where ![$ \sigma ∈ [ \sigma_0 , \sigma_1] $](form_542.png) . This is guaranteed by making the following check after
. This is guaranteed by making the following check after 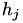 is determined
is determined
![\[ h_j = \left\{ \begin{array}{ll} \sigma_0 h_{j−1} & \mbox{ if } h_j < \sigma_0 h_{j−1} \\ \sigma_1 h_{j−1} & \mbox{ if } h_j > \sigma_1 h_{j−1} \\ h_j & \mbox{otherwise}. \end{array} \right. \]](form_543.png)
max_reduction_factor corresponds to 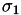
Referenced by set_predefined_parameters().
|
private |
min_reduction_factor corresponds to 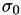
Referenced by set_predefined_parameters().
|
private |
Flag so that predefined parameters are used.
|
private |
Boolean variable that specifies if the three-point method is used with (true) or without (false) prediction, i.e.
the first iteration step is based on previous iteration steps.
 1.8.5
1.8.5