|
OpenFCST: The open-source Fuel Cell Simulation Toolbox
|
|
OpenFCST: The open-source Fuel Cell Simulation Toolbox
|
Functions | |
| double | R () |
Universal gas constant, ![$ R_{} = 8.314462176 \quad \left[ \frac{\text{J}}{\text{mol K}} \right] $](form_687.png) . More... . More... | |
| double | F () |
Faraday constant, ![$ F_{} = 9.648533992 \cdot 10^4 \quad \left[ \frac{\text{C}}{\text{mol}} \right] $](form_688.png) . More... . More... | |
| double | Pi () |
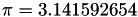 . More... . More... | |
| double | E0 () |
Permittivity of free space, ![$ \epsilon_0^{} = 8.854187818 \cdot 10^{-12} \quad \left[ \frac{\text{F}}{\text{m}} \right] $](form_690.png) . More... . More... | |
| double | K () |
Boltzmann constant, ![$ k_{} = 8.617332478 \cdot 10^{-5} \quad \left[ \frac{\text{eV}}{\text{K}} \right] $](form_691.png) . More... . More... | |
| double | K_SI () |
Boltzmann constant in SI units, ![$ k_{} = 1.3806488 \cdot 10^{-23} \quad \left[ \frac{\text{J}}{\text{K}} \right] $](form_692.png) . More... . More... | |
| double | N_A () |
Avogadro's constant, ![$ N_A = 6.022140857 \cdot 10^{23} \quad \left[ \frac{\text{molecules}}{\text{mol}} \right] $](form_693.png) . More... . More... | |
| const dealii::Tensor< 1, dim > | gravity_acceleration () |
Gravitational acceleration, ![$ \mathbf{g} = \{ g_{\alpha} \}_{\alpha = 1}^d \quad \text{such that} \quad \forall \alpha \neq d : \quad g_{\alpha} = 0 \quad \left[ \frac{\text{m}}{\text{sec}^2} \right] \quad \text{and} \quad g_d = -9.81 \quad \left[ \frac{\text{m}}{\text{sec}^2} \right] $](form_190.png) . More... . More... | |
| const dealii::SymmetricTensor < 2, dim > | unit_tensor () |
Unit tensor, 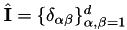 . More... . More... | |
| double | A_vk () |
Coefficient 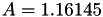 of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity). More... of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity). More... | |
| double | B_vk () |
Coefficient 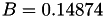 of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity). More... of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity). More... | |
| double | C_vk () |
Coefficient 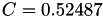 of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity). More... of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity). More... | |
| double | D_vk () |
Coefficient 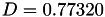 of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity). More... of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity). More... | |
| double | E_vk () |
Coefficient 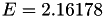 of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity). More... of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity). More... | |
| double | F_vk () |
Coefficient 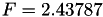 of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity). More... of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity). More... | |
| double | A_diff () |
Coefficient 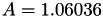 of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity). More... of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity). More... | |
| double | B_diff () |
Coefficient 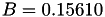 of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity). More... of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity). More... | |
| double | C_diff () |
Coefficient 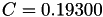 of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity). More... of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity). More... | |
| double | D_diff () |
Coefficient 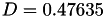 of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity). More... of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity). More... | |
| double | E_diff () |
Coefficient 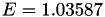 of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity). More... of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity). More... | |
| double | F_diff () |
Coefficient 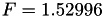 of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity). More... of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity). More... | |
| double | G_diff () |
Coefficient 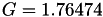 of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity). More... of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity). More... | |
| double | H_diff () |
Coefficient 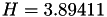 of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity). More... of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity). More... | |
| double | b_0 () |
Coefficient 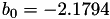 of the Springer-Zawodzinski-Gottesfeld water vapor saturation pressure formula. More... of the Springer-Zawodzinski-Gottesfeld water vapor saturation pressure formula. More... | |
| double | b_1 () |
Coefficient 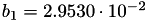 of the Springer-Zawodzinski-Gottesfeld water vapor saturation pressure formula. More... of the Springer-Zawodzinski-Gottesfeld water vapor saturation pressure formula. More... | |
| double | b_2 () |
Coefficient 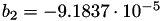 of the Springer-Zawodzinski-Gottesfeld water vapor saturation pressure formula. More... of the Springer-Zawodzinski-Gottesfeld water vapor saturation pressure formula. More... | |
| double | b_3 () |
Coefficient 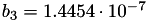 of the Springer-Zawodzinski-Gottesfeld water vapor saturation pressure formula. More... of the Springer-Zawodzinski-Gottesfeld water vapor saturation pressure formula. More... | |
| double | A11_visc_R1 () |
Coefficient 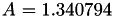 for the for the 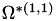 integrals formula (viscosity) between integrals formula (viscosity) between 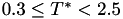 . More... . More... | |
| double | B11_visc_R1 () |
Coefficient 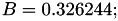 for the for the 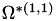 integrals formula (viscosity) between integrals formula (viscosity) between 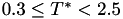 . More... . More... | |
| double | C11_visc_R1 () |
Coefficient 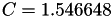 for the for the 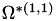 integrals formula (viscosity) between integrals formula (viscosity) between 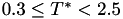 . More... . More... | |
| double | D11_visc_R1 () |
Coefficient 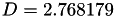 for the for the 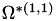 integrals formula (viscosity) between integrals formula (viscosity) between 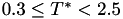 . More... . More... | |
| double | A11_visc_R2 () |
Coefficient 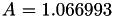 for the for the 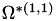 integrals formula (viscosity) between integrals formula (viscosity) between 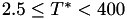 . More... . More... | |
| double | B11_visc_R2 () |
Coefficient 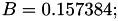 for the for the 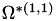 integrals formula (viscosity) between integrals formula (viscosity) between 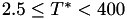 . More... . More... | |
| double | C11_visc_R2 () |
Coefficient 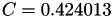 for the for the 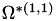 integrals formula (viscosity) between integrals formula (viscosity) between 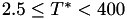 . More... . More... | |
| double | D11_visc_R2 () |
Coefficient 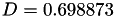 for the for the 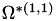 integrals formula (viscosity) between integrals formula (viscosity) between 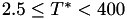 . More... . More... | |
| double | A22_visc_R1 () |
Coefficient 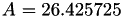 for the for the 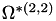 integrals formula (viscosity) between integrals formula (viscosity) between 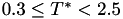 . More... . More... | |
| double | B22_visc_R1 () |
Coefficient 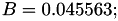 for the for the 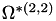 integrals formula (viscosity) between integrals formula (viscosity) between 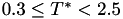 . More... . More... | |
| double | C22_visc_R1 () |
Coefficient 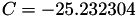 for the for the 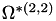 integrals formula (viscosity) between integrals formula (viscosity) between 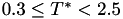 . More... . More... | |
| double | D22_visc_R1 () |
Coefficient 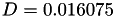 for the for the 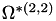 integrals formula (viscosity) between integrals formula (viscosity) between 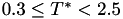 . More... . More... | |
| double | A22_visc_R2 () |
Coefficient 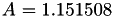 for the for the 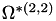 integrals formula (viscosity) between integrals formula (viscosity) between 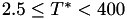 . More... . More... | |
| double | B22_visc_R2 () |
Coefficient 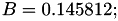 for the for the 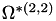 integrals formula (viscosity) between integrals formula (viscosity) between 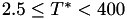 . More... . More... | |
| double | C22_visc_R2 () |
Coefficient 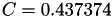 for the for the 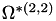 integrals formula (viscosity) between integrals formula (viscosity) between 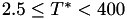 . More... . More... | |
| double | D22_visc_R2 () |
Coefficient 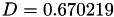 for the for the 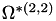 integrals formula (viscosity) between integrals formula (viscosity) between 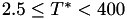 . More... . More... | |
|
inline |
Coefficient 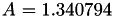 for the
for the 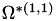 integrals formula (viscosity) between
integrals formula (viscosity) between 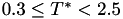 .
.
|
inline |
Coefficient 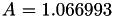 for the
for the 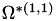 integrals formula (viscosity) between
integrals formula (viscosity) between 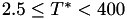 .
.
|
inline |
Coefficient 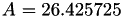 for the
for the 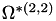 integrals formula (viscosity) between
integrals formula (viscosity) between 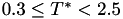 .
.
|
inline |
Coefficient 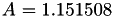 for the
for the 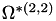 integrals formula (viscosity) between
integrals formula (viscosity) between 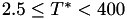 .
.
|
inline |
Coefficient 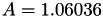 of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity).
of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity).
|
inline |
Coefficient 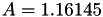 of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity).
of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity).
|
inline |
Coefficient 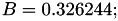 for the
for the 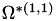 integrals formula (viscosity) between
integrals formula (viscosity) between 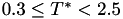 .
.
|
inline |
Coefficient 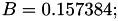 for the
for the 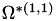 integrals formula (viscosity) between
integrals formula (viscosity) between 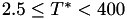 .
.
|
inline |
Coefficient 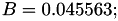 for the
for the 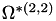 integrals formula (viscosity) between
integrals formula (viscosity) between 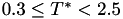 .
.
|
inline |
Coefficient 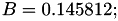 for the
for the 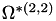 integrals formula (viscosity) between
integrals formula (viscosity) between 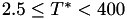 .
.
|
inline |
Coefficient 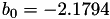 of the Springer-Zawodzinski-Gottesfeld water vapor saturation pressure formula.
of the Springer-Zawodzinski-Gottesfeld water vapor saturation pressure formula.
|
inline |
Coefficient 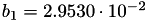 of the Springer-Zawodzinski-Gottesfeld water vapor saturation pressure formula.
of the Springer-Zawodzinski-Gottesfeld water vapor saturation pressure formula.
|
inline |
Coefficient 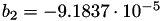 of the Springer-Zawodzinski-Gottesfeld water vapor saturation pressure formula.
of the Springer-Zawodzinski-Gottesfeld water vapor saturation pressure formula.
|
inline |
Coefficient 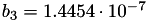 of the Springer-Zawodzinski-Gottesfeld water vapor saturation pressure formula.
of the Springer-Zawodzinski-Gottesfeld water vapor saturation pressure formula.
|
inline |
Coefficient 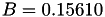 of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity).
of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity).
|
inline |
Coefficient 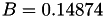 of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity).
of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity).
|
inline |
Coefficient 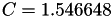 for the
for the 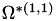 integrals formula (viscosity) between
integrals formula (viscosity) between 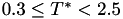 .
.
|
inline |
Coefficient 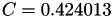 for the
for the 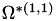 integrals formula (viscosity) between
integrals formula (viscosity) between 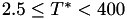 .
.
|
inline |
Coefficient 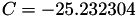 for the
for the 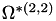 integrals formula (viscosity) between
integrals formula (viscosity) between 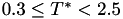 .
.
|
inline |
Coefficient 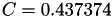 for the
for the 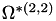 integrals formula (viscosity) between
integrals formula (viscosity) between 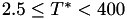 .
.
|
inline |
Coefficient 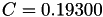 of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity).
of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity).
|
inline |
Coefficient 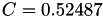 of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity).
of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity).
|
inline |
Coefficient 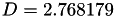 for the
for the 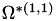 integrals formula (viscosity) between
integrals formula (viscosity) between 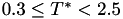 .
.
|
inline |
Coefficient 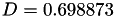 for the
for the 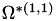 integrals formula (viscosity) between
integrals formula (viscosity) between 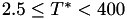 .
.
|
inline |
Coefficient 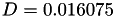 for the
for the 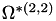 integrals formula (viscosity) between
integrals formula (viscosity) between 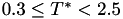 .
.
|
inline |
Coefficient 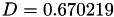 for the
for the 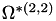 integrals formula (viscosity) between
integrals formula (viscosity) between 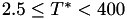 .
.
|
inline |
Coefficient 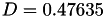 of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity).
of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity).
|
inline |
Coefficient 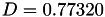 of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity).
of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity).
|
inline |
Permittivity of free space, ![$ \epsilon_0^{} = 8.854187818 \cdot 10^{-12} \quad \left[ \frac{\text{F}}{\text{m}} \right] $](form_690.png) .
.
Referenced by FuelCellShop::MicroScale::AgglomerateBase::AgglomerateBase().

|
inline |
Coefficient 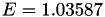 of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity).
of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity).
|
inline |
Coefficient 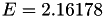 of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity).
of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity).
|
inline |
Faraday constant, ![$ F_{} = 9.648533992 \cdot 10^4 \quad \left[ \frac{\text{C}}{\text{mol}} \right] $](form_688.png) .
.
Referenced by FuelCellShop::MicroScale::AgglomerateBase::AgglomerateBase(), FuelCellShop::Kinetics::BaseKinetics::BaseKinetics(), and FuelCellShop::Equation::ReactionHeat::initialize_factors().
|
inline |
Coefficient 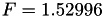 of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity).
of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity).
|
inline |
Coefficient 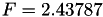 of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity).
of the Neufeld-Jansen-Aziz collision integrals formula (viscosity and thermal conductivity).
|
inline |
Coefficient 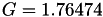 of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity).
of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity).
|
inline |
Gravitational acceleration, ![$ \mathbf{g} = \{ g_{\alpha} \}_{\alpha = 1}^d \quad \text{such that} \quad \forall \alpha \neq d : \quad g_{\alpha} = 0 \quad \left[ \frac{\text{m}}{\text{sec}^2} \right] \quad \text{and} \quad g_d = -9.81 \quad \left[ \frac{\text{m}}{\text{sec}^2} \right] $](form_190.png) .
.
References dim.
|
inline |
Coefficient 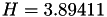 of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity).
of the Neufeld-Jansen-Aziz collision integrals formula (diffusivity).
|
inline |
Boltzmann constant, ![$ k_{} = 8.617332478 \cdot 10^{-5} \quad \left[ \frac{\text{eV}}{\text{K}} \right] $](form_691.png) .
.
Referenced by FuelCellShop::Kinetics::BaseKinetics::BaseKinetics().

|
inline |
Boltzmann constant in SI units, ![$ k_{} = 1.3806488 \cdot 10^{-23} \quad \left[ \frac{\text{J}}{\text{K}} \right] $](form_692.png) .
.
|
inline |
Avogadro's constant, ![$ N_A = 6.022140857 \cdot 10^{23} \quad \left[ \frac{\text{molecules}}{\text{mol}} \right] $](form_693.png) .
.
|
inline |
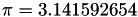 .
.
Referenced by FuelCellShop::MicroScale::SphericalAgglomerateGeometry::SphericalAgglomerateGeometry().

|
inline |
Universal gas constant, ![$ R_{} = 8.314462176 \quad \left[ \frac{\text{J}}{\text{mol K}} \right] $](form_687.png) .
.
Referenced by FuelCellShop::MicroScale::AgglomerateBase::AgglomerateBase(), FuelCellShop::Kinetics::BaseKinetics::BaseKinetics(), FuelCell::OperatingConditions::get_anode_gas_density(), FuelCell::OperatingConditions::get_cathode_gas_density(), and FuelCellShop::Equation::LiquidSourceEquation< dim >::get_temp_related_parameters().
 1.8.5
1.8.5